Arcadio abrió la puerta de su recámara sumido en algunas cavilaciones, pero apenas dio un paso fue devuelto violentamente a la realidad por un extraño sonido: había pisado uno de sus CD. Revisó la superficie plateada y aparentemente no se había dañado de manera relevante, al menos no se veía más rayada de lo que ya estaba. Cuando lo puso, las primeras tres canciones se oyeron bien pero, a 2 minutos y 17 segundos de empezada la cuarta, el disco se trabó. Éste probablemente no sea el término adecuado, pero es el que resulta más acertado intuitivamente. El aparato reproducía la misma sílaba de la canción una y otra vez, como si tuviera hipo, hasta que Arcadio presionaba el botón de adelantar para forzarlo a "pasar el bache", por decirlo así, y luego continuaba sin contratiempos durante un rato.
En realidad, Arcadio fue testigo de lo que ocurre cuando un aparato reproductor de CD se topa con un error. En los discos compactos se almacenan datos con cadenas de bits grabados sobre su superficie. Con el fin de que el disco no sea tan delicado en su manejo y resulte posible reproducirlo con fidelidad a pesar de que tenga partículas de polvo, huellas digitales, manchas o pequeñas rayaduras inevitables, cada una de estas cadenas de bits va codificada usando una representación que permite al aparato reproductor "darse cuenta" de ciertos errores en los bits leídos y corregirlos. Cada partícula de polvo o huella digital puede afectar potencialmente algunos de los bits leídos y cambiarlos; reproducir los datos leídos suponiéndolos inmaculados resultaría un desastre ininteligible. Por tanto, los datos se codifican de tal forma que, luego de ser leídos, el aparato reproductor pueda verificarlos para determinar: a] si son correctos o b] si no lo son y pueden ser corregidos, es decir, qué hay que cambiarles para corregirlos.
El algoritmo estándar de los reproductores de discos compactos de audio indica que si se detectan errores en los datos y éstos no pueden ser corregidos, entonces se debe proceder a enviar al dispositivo de audio la última señal correcta leída. De allí que parezca que el disco se "atora" o "tiene hipo". Esta misma idea se utiliza en casi todos los contextos en los que es necesario almacenar o transmitir información de manera confiable. En el disco duro de cualquier computadora los datos se almacenan en bloques de ceros y unos, y éstos van sucedidos de un código que permite verificar lo que se leyó y corregir un cierto número de errores. Prácticamente todas las transmisiones de televisión digital, de telefonía, satelitales, de internet y los datos almacenados en DVD, por ejemplo, se codifican usando códigos detectores y correctores de error.
El objetivo es, por supuesto, garantizar, en la medida de lo posible, que la información que se recupera del medio de transmisión o almacenamiento sea exactamente la misma que se envió o se almacenó originalmente. Se da por sentado que el canal de transmisión o el medio de almacenamiento no es infalible, es decir, que se presupone la existencia de errores que pueden alterar lo que se almacena o transmite por un canal. A esto se le llama, genéricamente, ruido.
En la teoría de la información se estudian diversos tipos de ruido. Sin embargo, la característica más relevante del ruido es que es aleatorio, porque no se puede saber de antemano qué bits serán alterados. En el modelo de ruido más sencillo se supone que un bit tiene la misma probabilidad de ser alterado que cualquier otro, y que la alteración de uno de ellos no tiene nada que ver con la posible alteración del siguiente. A esto suele llamársele ruido blanco. Un ejemplo de ruido blanco es el "hormigueo gris" que queda en la pantalla cuando termina la programación de las transmisiones por televisión.
La clave para lograr "darse cuenta" de que han ocurrido errores y el primer paso para saber cuáles son los datos incorrectos es añadirle a la información cierta redundancia. La idea general para hacer esto es poseer un catálogo de palabras suficientemente amplio para decir lo que sea necesario, pero que al mismo tiempo sean palabras suficientemente diferentes entre sí. Será más fácil comprender esta situación con un ejemplo.
Curiosidades
Las sondas espaciales que el hombre ha enviado a explorar los confines del Sistema Solar envían a la Tierra las imágenes fotográficas que capturan, codificadas con mecanismos que permiten detectar y corregir errores. Las transmisiones de estas sondas están sometidas a perturbaciones ocasionadas por las emisiones electromagnéticas del Sol, lo que suele llamarse "viento solar". Ésta es una célebre fotografía de Saturno tomada por la sonda Voyager 1 en 1979.
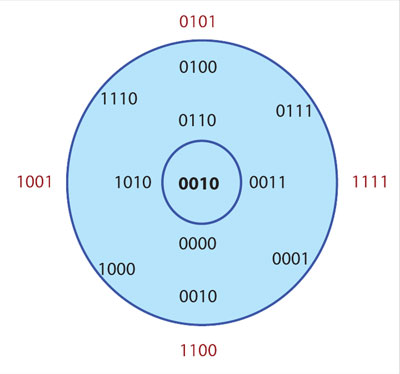
Supongamos que se necesita comunicar 16 cosas diferentes. Si hay que decir 16 cosas diferentes se pueden usar cuatro bits para codificarlas, dado que 24 = 16. Ahora, si se desea transmitir datos a un compañero, cada uno de éstos será una de esas 16 cosas que se han representado con cuatro bits. Lo único que debe hacerse es enviar el código —es decir, cuatro bits— por cada cosa que se desea comunicar al receptor. De manera que aunque se tengan varias cosas que decir, sólo se envían cuatro bits por cada una. Complicando las cosas un poco, asumiendo que el canal de comunicación que se usa para transmitirle al receptor tiene ruido y que éste puede echar a perder algunos de los bits enviados, bien pudiera ser que se envíe la palabra 0010 y un compañero reciba 0011 porque se alteró el último bit. En la figura 6 se observa cómo mientras más errores se introducen, más se aleja el mensaje de la palabra original. El primer círculo contiene palabras con un error, el segundo con dos, etcétera.
¿Puede el receptor de la palabra 0011 percatarse de que ha ocurrido un error? Él no sabe qué se le envió, la única manera de comunicarse con el remitente es a través del canal que se está usando. La respuesta es no. El código que el receptor recibe es tan válido como el que se le envió; el receptor puede, con toda confianza, suponer que lo que recibió es lo que efectivamente se le mandó porque no tiene modo de distinguir las palabras del código correctas de las que no lo son. El problema es que se utilizó todo el poder de expresividad posible de cuatro bits para crear las palabras del código que se quería decir, y ninguna palabra de cuatro bits es inválida. No hay espacio entre las palabras.
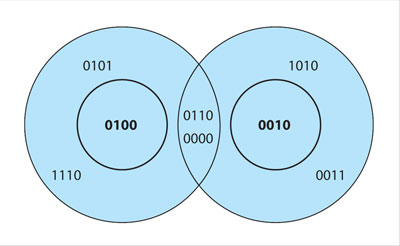
Para poder distinguir cuando algo está mal no se debe usar todo el poder expresivo del código; es necesario que algunas de las posibles secuencias, de la longitud que se usen, sean inválidas. Éstas forman "huecos" y logran que entre las palabras del código haya suficiente distancia. En la figura 7 se observa que si se incluyen en el código las palabras 0100 y 0010, pero no las de alrededor de éstas, es posible detectar si hubo un (sólo uno) error. Las palabras 0101, 1110, 0110, 0000, 1010 o 0011 no serían válidas. Pero aunque así se puede detectar un error, no es posible corregirlo; si se recibe 0000, no hay manera de saber si la palabra enviada fue 0100 o 0010, ya que no hay manera de saber si fue el segundo o el tercer bit el que cambió.
Si sólo se necesita expresar ocho cosas diferentes y se pueden usar los mismos cuatro bits, hay más espacio. Suponiendo que se usan como catálogo de palabras de código válidas todas las que terminan con 0. Si ahora se envía 0110 y del otro lado se recibe 0111, el receptor sí puede darse cuenta de que algo se estropeó en el canal, porque sabe que no es posible enviar algo que termine con "1" pues no está en el catálogo de palabras válidas. A los tres bits estrictamente necesarios para expresar ocho cosas se les ha añadido uno más; entonces ya se puede hacer algo con respecto a los errores. Desgraciadamente, si se echa a perder el segundo bit, como se mencionó antes, y se recibe 0010, el receptor no podrá darse cuenta del error. No basta entonces con añadir datos, también hay que cuidar que las distancias entre las palabras del código estén bien distribuidas; que los huecos rodeen bien a todas las palabras.
Un esquema similar al que se usó en el párrafo anterior ha sido muy usado a lo largo de la historia. Se trata de añadir un bit a cada palabra del código, de tal forma que siempre se complete un número par o impar. Según se elija un número par o impar, el sistema adquiere su nombre. Por ejemplo, si se desean codificar 16 datos posibles, se emplearán cuatro bits para cada uno de ellos, pero esta vez cuando la palabra de cuatro bits tenga un número impar de unos se le agregará otro más al final y cuando no sea así se le agregará un cero. Este esquema, claro está, es el de paridad par. Así, la palabra 0110 se convierte en 01100, el último cero significa que la palabra completa de cinco bits tiene un número par de bits "prendidos", es decir, con valor 1, en los primeros cuatro. En cambio, si deseamos enviar 0010, deberíamos enviar 00101, dado que el quinto bit indica que se tiene un número impar de unos en los primeros cuatro bits. Ahora sí, el receptor se percatará de que algún bit fue cambiado accidentalmente en el canal durante la transmisión.
Con un esquema de verificación de paridad es posible darse cuenta de que ha ocurrido un error —o, mejor dicho, un número impar de errores— en los bits transmitidos, pero cuando el número de errores es par, pasarán desapercibidos. Para poder detectar un mayor número de errores o, mejor aún, corregirlos, se debe añadir más redundancia.
La clave para poder corregir errores es hacer que las palabras del código que se usan para enviar los datos sean muy diferentes entre sí. Si dos palabras se parecen mucho, por ejemplo: 0110101 y 0110001, basta con que ocurra un error en el quinto bit para que una se convierta en la otra y el receptor del mensaje la dé por buena. Cuanto mayor sea la distancia entre las palabras del código, mayor será el número de errores que deben ocurrir en el canal para que se convierta en otra palabra válida. Por esto, una de las cualidades más importantes de los códigos detectores y correctores de errores es la medida de la diferencia mínima entre sus palabras, a lo que suele llamársele distancia mínima del código.