La relación entre la música y las matemáticas era ya conocida por las culturas caldea, egipcia, babilónica y china; sin embargo, hasta la escuela pitagórica, en la Grecia del siglo VI a.C., fue cuando estas actividades humanas quedaron unidas para siempre por la teoría de la cuerda vibrante.
Si se hace vibrar una cuerda, el sonido que produce depende de su longitud, su grosor y su tensión. El tono es más agudo conforme la cuerda se acorta. Lo que se descubrió en la escuela pitagórica es que, al dividir la cuerda, hay proporciones que producen sonidos más agradables que otros. Por ejemplo, si se divide la cuerda justo a la mitad, la vibración tiene un tono de una octava mayor que la producida por la longitud original. Por ello, la octava juega un papel fundamental en nuestra comprensión de la música.
Los pitagóricos establecieron cuatro intervalos o relaciones entre las longitudes de las cuerdas que producían las únicas consonancias permitidas, es decir, aquellos sonidos que podían escucharse simultáneamente con un efecto agradable. Para producir todas las notas musicales sólo se tienen estos cuatro intervalos y sus combinaciones. El papel fundamental de las fracciones en la música era, sin duda, una de las razones por las cuales Pitágoras consideraba que la esencia de la realidad sólo podía expresarse por medio de números.
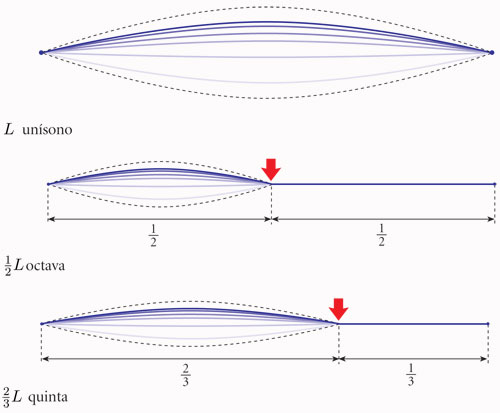
La teoría de la cuerda vibrante se puede resumir de la siguiente manera: si se tensa una cuerda y se hace vibrar, emite un sonido de un tono; si se hace vibrar la mitad de la cuerda, el tono aumentará una octava; si se hace vibrar dos tercios de la cuerda, el tono estará un quinto por encima del que produjo la cuerda entera; si se hace vibrar tres cuartos de la cuerda original, el tono estará una cuarta por arriba del tono original.
Al vibrar, una cuerda o cualquier otro cuerpo transmite su vibración al aire que la rodea; estas alteraciones en la densidad del aire se propagan en forma de ondas y cuando llegan a nuestros oídos, las percibimos como sonido.
Una de las características más importantes de una onda sonora es su frecuencia, que se mide en hertzios —un hertzio equivale a una oscilación por segundo—. El oído de un niño sano percibe sonidos de 12 a 20 000 hertzios pero, al envejecer, este rango disminuye, especialmente para la percepción de sonidos agudos.
Para darnos una idea diremos que un bajo, es decir, la voz humana más grave, canta en el rango de 80 a 300 hertzios y una soprano, con voz muy aguda, alcanza un rango entre 220 a 1 000 hertzios.
Las notas musicales son sonidos puros en los que únicamente está presente una frecuencia. La relación que existe entre la frecuencia de distintos sonidos es muy importante y se muestra en la siguiente tabla:
La razón de las frecuencias se llama intervalo o distancia y es el cociente entre las frecuencias. Por ejemplo, el intervalo entre fa y la es, igua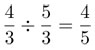
l al intervalo entre do y mi.
Si silbamos con los labios, el sonido es casi de una sola frecuencia, pero si hablamos o se toca un instrumento se producen varias frecuencias a la vez. Usualmente hay una frecuencia predominante, la principal, y otras secundarias de menor intensidad que tienen cierta relación matemática con la frecuencia principal y se llaman armónicos. La intensidad con la cual se emiten los armónicos hace que los instrumentos musicales suenen diferentes entre sí.
Aunque los pitagóricos nunca hablaron de armónicos, determinaron que las cuerdas de longitudes con razones 1 : 2 y 2 : 3 producían combinaciones de sonidos muy agradables y, a partir de estas proporciones, construyeron una escala musical.
Los pitagóricos fueron los primeros en establecer la música como una disciplina matemática, una de las siete fundamentales que los jóvenes tenían que estudiar en la escuela. Las relaciones que se establecieron hace más de 2 500 años entre las matemáticas y la música están vigentes y siguen presentes en cualquier sala de conciertos. Una vez que un descubrimiento matemático se ha establecido, queda para siempre en la vida cotidiana. ¡Que no nos extrañe que los violines se afinen hoy día como los habrían afinado los miembros de la escuela de Pitágoras!
