En el Renacimiento, los artistas plásticos acabaron de establecer los principios técnicos de la perspectiva. La idea básica es que un cuadro representa mejor la realidad si se le concibe como una ventana —a través de la cual se ve el paisaje— en la que se plasma lo que el pintor ve. Geométricamente, lo anterior equivale a proyectar al plano del lienzo lo visible —representado con su color— desde un punto fijo: el ojo del pintor que será posteriormente el del obsevador. Entonces resulta que las escalas de las cosas se hacen más chicas conforme están más lejos, y que líneas rectas que en la realidad son paralelas deben dibujarse como líneas que concurren a un punto llamado su punto de fuga.
Las líneas reales se proyectan en líneas al lienzo, pues son la intersección del lienzo con el plano que une la línea real con el ojo. Resulta que los puntos de fuga de todos los haces paralelos en un plano forman una línea: su línea al infinito; por ejemplo, la línea al infinito del piso es el horizonte en el lienzo, al cual se fugan todas las líneas horizontales. Supongamos que queremos dibujar en perspectiva un edificio que se encuentra enfrente y a nuestra izquierda. El plano paralelo a su fachada que pasa por nuestro ojo se interseca con el lienzo en su línea al infinito: cualquier cosa en el plano de la fachada se verá a la izquierda de esta línea, como se aprecia en la figura 4.38 b.
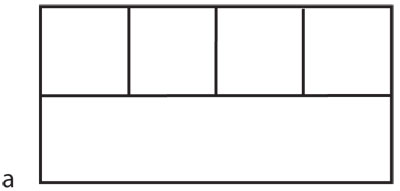
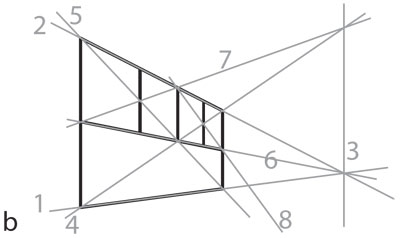
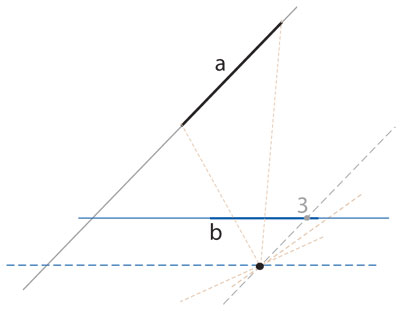
Al proyectar planos a planos desde un punto, resulta natural y teóricamente indispensable considerar que sus líneas al infinito constan de un punto de fuga por cada haz paralelo. Al plano euclidiano con un nuevo punto para cada dirección, en el que concurren las paralelas correspondientes y forman una nueva línea —al infinito— se le llama plano proyectivo; tiene un grupo de transformaciones asociado, las transformaciones proyectivas, que son las que preservan líneas. Un ejemplo es el de la figura 4.38 a, que manda la fachada hacia su perspectiva en 4.38 b. En este caso, basados en que las líneas van en líneas, sólo se hicieron los trazos necesarios para reconstruir la fachada, pero la transformación está definida en todo el plano, es decir, se puede decidir cuál debe ser la imagen de cualquier punto. En términos de proyecciones y volviendo a pensar en el paradigma del pintor, en la figura 4.39 la fachada es parte de un plano (a) y el lienzo es parte de otro plano (b); al pintor sólo le interesa lo que está enfrente pero, matemáticamente, se considera todo: lo que está atrás del pintor se proyecta del otro lado de la línea al infinito, de (a) vista en (b).
El plano elíptico y el plano proyectivo están en correspondencia natural. Para entender lo anterior, se considera al plano tangente a la esfera en su polo norte y, después, se proyecta desde el centro de la esfera. Las líneas se corresponden, pues en ambos casos son intersecciones de planos por el centro de proyección. Los puntos en el ecuador de la esfera van hacia el punto correspondiente en la dirección de la línea al infinito del plano proyectivo.
De hecho, a estos dos planos se les piensa como el mismo espacio y lo que los distingue es el grupo de transformaciones que se consideran: en el plano elíptico se juega sólo con las transformaciones rígidas y, entonces, se puede hablar de distancias, ángulos y áreas; en el proyectivo se usan todas aquellas transformaciones proyectivas o colineaciones, que de hecho son muchas.
Aunque aquí hemos hablado de la geometría proyectiva en forma sintética, también se puede trabajar analíticamente —es decir, con coordenadas— y ésta es hoy día una de las herramientas básicas para el despliegue de la realidad virtual en las computadoras.