Se considera a Girard Desargues (1591-1661) el padre de la geometría proyectiva, pues sentó sus bases y demostró los primeros teoremas. Sin embargo, éstos no fueron retomados por otros matemáticos durante los dos siglos siguientes, quizá porque su contemporáneo, René Descartes (1596-1650) atrajo los reflectores de la historia al "coordinatizar" el plano euclidiano. Descartes estableció la correspondencia entre parejas ordenadas de números reales y puntos en el plano euclidiano; con ello, nace la geometría analítica y la posibilidad de usar nuevos métodos en la geometría. Más aún, también se abre la puerta para trabajar en otras dimensiones.
Si se describe el plano con parejas de números y el espacio con ternas, al considerar todas las cuartetas de números reales, tendremos el espacio de dimensión cuatro. Estos espacios se denotan R2 R3 y R4 respectivamente. No hay que pararse en cuatro: para cualquier número n se puede definir el espacio euclidiano de n dimensiones como el conjunto de n -adas ordenadas de números reales:
Aunque no se pueda ver o se dude de su existencia en el sentido físico, matemáticamente está ahí, para ser explorado. Por ejemplo, se pueden definir líneas, segmentos y distancias de manera que se extiende naturalmente a los conceptos euclidianos para dimensiones 2 y 3.
A mediados del siglo XIX, Bernhard Riemann amplía, aún más, la noción de "espacio". Ciertos subconjuntos de RN son especiales, pues localmente se parecen a o se pueden modelar como Rn, para alguna n < N; se les llama ahora variedades de dimensión n. Por ejemplo, las superficies lisas —n = 2 — en el espacio —N = 3—, son variedades de dimensión 2; o bien, los puntos que equidistan de uno dado en RN son las esferas de dimensión N - 1. Y, por vivir en RN, heredan una geometría explícita.
Se puede medir la distancia entre dos puntos como la longitud más corta de las trayectorias que los unen dentro de la variedad; y a estas trayectorias más cortas o eficientes para viajar se les llama geodésicas. Por ejemplo, si tomamos una esfera en R3 o en RN, sus geodésicas son los círculos máximos o intersecciones de planos que pasan por su centro. Riemann observa que ahí hay muchísimos espacios donde se puede hacer geometría, y establece las bases y herramientas para hacerla: lo que ahora llamamos geometría riemanniana
Cuando a principios del siglo XX, Albert Einstein le demuestra al mundo que el Universo debe concebirse como algo de dimensión cuatro y, además, no euclidiano sino con curvatura producida por la masa, tenía ya la herramienta matemática para hablar de ello.
Otro personaje importante en la geometría del siglo XIX fue Sophus Lie. Estudió los grupos de transformaciones de los espacios euclidianos multidimensionales y observó que son variedades; son grupos continuos llamados grupos de Lie. El ejemplo más sencillo es el círculo, pensado como las rotaciones del plano alrededor del origen y, a su vez, como variedad de dimensión 1. Los grupos de Lie han resultado ser una herramienta indispensable para la física del siglo xx, sobre todo para la física cuántica.
Hacia el final del siglo XIX, cuando la geometría se convulsionó y expandió en múltiples direcciones, Felix Klein trató de resumir la definición de geometría diciendo que "es el estudio de los invariantes de un espacio bajo un grupo escogido de sus transformaciones". Pongamos un ejemplo de esta idea, retomando el modelo del plano hiperbólico del propio Klein. El espacio dado es el interior del disco —como se muestra en la figura 4.34—; si lo pensamos dentro del plano proyectivo —que contiene al euclidiano—, podemos considerar todas las transformaciones proyectivas que lo dejan en su lugar: éste es el grupo de transformaciones hiperbólicas. Entonces, resulta que cualquier punto del interior se puede mover a cualquier otro; que el espacio es homogéneo y que los "invariantes", como distancia y ángulo, se pueden construir a partir del grupo.
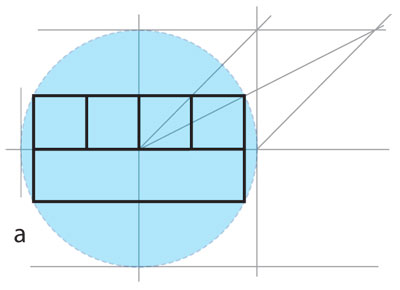
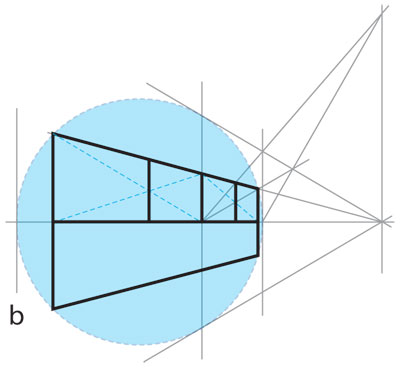
Para ver un ejemplo de una transformación hiperbólica, además de las obvias, las rotaciones, supongamos que la fachada de la figura 4.38.a) está inscrita en el círculo del modelo de Klein y queremos trasladarla —como figura hiperbólica— en su línea media horizontal. Basados en que las líneas tangentes al círculo deben ir a líneas tangentes al mismo, pues éste se queda, como conjunto, en su lugar —ésa es la definición de transformación hiperbólica—; una vez fijado el punto donde va el centro de la fachada, con unos cuantos trazos más se obtiene su traslación hiperbólica, como se observa en la figura 4.40.