Ya los hindúes se daban a la tarea de proponer y resolver ecuaciones desde el siglo VIII a.C. En una ecuación aparecen variables y constantes, que se enlazan con operaciones para formar los dos términos en ambos lados de la ecuación. Por ejemplo, en la ecuación:
x + 3 = 6, (10)
x es una variable, los números 3 y 6 son constantes y hay una sola operación involucrada, que es la suma. Nuestras constantes serán números enteros o racionales o, a veces, reales.
Resolver la ecuación significa encontrar los valores para las variables, de manera que la ecuación sea válida. Si sustituimos x = 2 en la ecuación 10, ésta se transforma en:
5 = 6
que, evidentemente, es falso. En cambio, si sustituimos x = 3, obtenemos la ecuación:
6 = 6
que es correcta. Por ello, x = 3 es solución de la ecuación 10 y x = 2, no lo es.
También hay ecuaciones que involucran funciones. Por ejemplo:
cos (π x) = x2 (11)
es una ecuación que involucra dos funciones: coseno y elevar al cuadrado. Sin embargo, estas dos funciones no juegan el mismo papel, pues podemos entender al cuadrado de x como el producto de x con x misma, lo que equivale a decir que x2 = x ∙ x. En cambio, la función coseno no se puede reducir a una expresión sencilla que sólo involucre las operaciones básicas de sumar, restar, multiplicar y dividir.
Las ecuaciones algebraicas son aquellas que sólo involucran variables, constantes y operaciones básicas. Veamos algunos ejemplos sencillos.
Si en (10) cambiamos los valores de las constantes, cambiamos la ecuación pero no su estructura. De manera más general, podemos considerar ecuaciones que tienen la forma:
ax + b = 0, (12)
donde a y b son constantes dadas. Si en una ecuación se indican constantes con una variable, se habla de parámetros. La ecuación (12) se llama ecuación lineal y podemos resolverla siempre que a no sea cero, en cuyo caso la solución es:
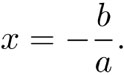
Un poco más complicada es la ecuación cuadrática:
ax2 + bx + c = 0, (13)
donde x es la variable mientras que a, b y c son los parámetros, es decir, constantes. Esta ecuación puede tener hasta dos soluciones:
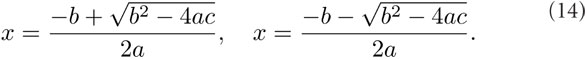
Estas fórmulas se obtienen con un truco para completar cuadrados y que se explicará con detalle más adelante.
El número de soluciones depende del valor del discriminante D = b2 – 4ac, es decir, del valor de lo que está dentro de la raíz cuadrada. Si D = 0, entonces sólo hay una solución: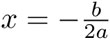 
. Cuando D > 0, las dos soluciones (14) son distintas.
Un caso interesante es cuando D > 0 pues, a partir de la fórmula, se tendría que calcular la raíz cuadrada de un número negativo. Pero no existe número real λ tal que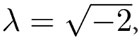 
, ya que al elevar al cuadrado se obtendría λ2 = -2. ¡Es imposible tener el lado izquierdopositivo y el derecho negativo! Por ello, podríamos decir que la ecuación (13) no tiene solución. También podríamos tratar de extender la noción de los números e incluir las raíces de números negativos. Aunque sea algo bastante raro, sorprendentemente, funciona muy bien. La humanidad tardó siglos en aceptar estos nuevos números que, en la actualidad, son muy comunes. Los números complejos son un concepto difícil, así que para entenderlos iremos despacio.
