Todo parte del supuesto de que existe un número i, que llamaremos unidad imaginaria —por razones históricas—, tal que i2 = -1. Lo que buscamos es extender los números reales a un nuevo conjunto más grande, llamado el de los números complejos, de manera muy similar a como se extienden los números naturales a los enteros, al añadir los negativos. Así, debemos poder formar nuevos números —por lo pronto, los marcamos con negritas para distinguirlos— como:
x = 2 + i, y = 3 2i
Con ellos, debemos poder calcular productos:
x ∙ y = (2 + i) (3 – 2i)
Pero entonces, necesitamos que los nuevos números satisfagan las mismas leyes que los reales, respecto a la adición y el producto. En este caso, podríamos seguir:
Como se observa en el ejemplo anterior, obtuvimos de nuevo la forma a + bi, donde a y b son dos números reales. Esto, en efecto, siempre es así y podemos hacer lo mismo que en el ejemplo para ver que:
(a + bi) ∙ (c + di) = (ac = bd) + (ad + bc)i (15)
La suma es más fácil:
x + y = (2 + i) + (3 – 2i)
= (2 + 3) + (i – 2i) por conmutividad y asociación de la adición
= 5 – i
En general, se tiene que:
(a + bi) + (c + di) = (a + c) + (b + d)i.
También podemos restar:
(a + bi) – (c + di) = (a – c) + (b – d)i,
y para ver que podemos dividir, tenemos que hacer un par de maniobras adicionales. Dividir entre 2 es lo mismo que multiplicar por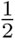 
, esto es, por el multiplicativo inverso de 2. En general, esperamos que:
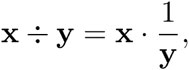
y como sabemos multiplicar gracias a la fórmula (15), es suficiente calcular el inverso multiplicativo de cualquier número complejo con forma y = c + di. Para ello, observamos que:
(c + di) ∙ (c – di) = (c2 – d (–d)) + 0i = c2 + d2,
es un número real que no es cero si y ≠ 0 + 0i. Por ello, si y ≠ 0 tenemos que:
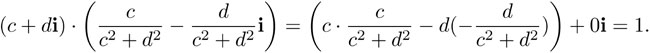
Por consiguiente, se obtiene la siguiente fórmula para la formación de inversos multiplicativos:
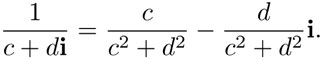
Para resumir, debemos considerar que todo parte de dos supuestos:
• Existe un número i, que llamaremos unidad imaginaria, tal que i2 = -1.
• El número i y todos los nuevos números satisfacen las mismas leyes que involucran la adición y la multiplicación que los números reales.
Entonces, los números complejos son de la forma a + bi, con y reales a y b que cumplen las siguientes leyes:
