En marzo de 1785, don Diego Ruiz, recolector de impuestos del gobierno español, buscaba sembradíos clandestinos de tabaco en la selva tropical a las afueras de Papantla, Veracruz. No sabemos si halló lo que buscaba, pero lo que sí encontró fue una pirámide de grandes dimensiones que hoy forma parte del sitio arqueológico conocido como El Tajín. Hasta 1938 empezó la limpieza y reconstrucción del lugar, formado por varios edificios y canchas de juegos de pelota. La peculiaridad del sitio es una pirámide que tiene, en cada uno de sus costados, numerosos nichos a partir de los cuales toma su nombre. Se dice que tiene 365 nichos, tantos como los días del año, por lo que se piensa que la pirámide cumplió alguna función similar a la de un calendario.
¿Cómo se pueden acomodar 365 nichos en una pirámide? Esa pregunta se la hicieron con toda seguridad los totonacas antes de empezar con la construcción de la pirámide.
Aunque acomodar nichos en una pirámide no sea un problema de nuestra vida cotidiana, sí lo fue, al menos, para los sacerdotes y sabios encargados de aquella construcción. Si bien las matemáticas del bachillerato son muy pocas veces útiles de manera directa en la vida cotidiana, nos permiten asomarnos de una forma distinta a nuestra cultura: mediante una comprensión más profunda de la tecnología que nos rodea, nos hacen partícipes de los logros de la humanidad.
Volviendo al problema de acomodar nichos, primero hay que observar que 365 no es divisible entre 4, es decir, no es posible acomodar el mismo número de nichos en cada costado tal que en total sumen 365. Pero el número 365 es divisible entre 5 : 365 = 5 · 73. Entonces habría que construir una pirámide con cinco lados, y de ese tipo no hay en México; con seguridad, esto no les hubiera parecido una buena idea.
Si se coloca un nicho en la punta quedan 364 nichos para ser acomodados en los cuatro costados de una pirámide auténtica, como la de El Tajín. Dado que 364 = 4 · 91, habría 91 nichos en cada lado. La distribución de los nichos en cada lado de la pirámide se puede hacer de muchas maneras; por ejemplo, se podrían acomodar 40 nichos en el nivel más bajo, 30 en el que sigue y 21 en el tercero y último, pero quedaría una pirámide muy ancha con sólo 3 niveles. Además, pasaría que del nivel más ancho al del medio se disminuye el número de nichos en 10, mientras que del medio al último se disminuye en 9 . Esto ocasionaría que los nichos en el último nivel tendrían que ser más pequeños que el resto o que la pirámide no tuviera un borde regular. Dicho lo anterior, sería mejor que de nivel en nivel siempre disminuyera el mismo número de nichos. Por ejemplo, podríamos pensar en la sucesión 3, 5, 7, 9, 11, 13, 15, 17 para el número de nichos en cada nivel. Esto nos daría una pirámide regular con 3 + 5 + 7 + 9 + 11 + 13 + 15 + 17 = 80 nichos. Si agregamos otro nivel, éste tendrá 19 nichos y se excedería de los 91 que deben ser. Al parecer, la distribución de 365 nichos en una pirámide no es un problema tan sencillo.
Las sucesiones de este estilo se llaman sucesiones aritméticas y han sido estudiadas. Entre las más famosas está, por ejemplo, aquella que empieza con uno y aumenta siempre de uno en uno: 1, 2, 3, 4, 5, 6, 7, 8. Se cuenta que un maestro de matemáticas de Alemania pidió a sus alumnos calcular la suma de los primeros 100 números para tenerlos ocupados por un buen rato; uno de ellos entregó su respuesta después de un minuto, mientras los demás necesitaron casi la hora completa. La gran sorpresa fue que la primera respuesta era de las pocas correctas, resuelta por Carl Friedrich Gauss, un joven que el mundo reconocería después como uno de los matemáticos más influyentes de todos los tiempos.
No es que Gauss calculara muy rápido, sino que usó un truco que él inventó: si se suman los números en pares, tomándolos de los extremos así:
(100 + 1) + (99 + 2) + (98 + 3) + . . . + (53 + 48) + (52 + 49) + (51 + 50),
entonces, cada par suma 101 y hay 50 pares. Así que el resultado es:
101 · 50 = 5 050.
Los números siguientes:
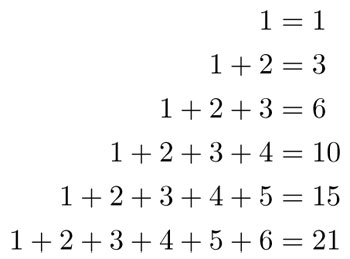
se llaman números triangulares. También el 91 es triangular:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 = 91.
Pero una pirámide con los nichos acomodados de esta manera tendría 14 niveles y sería muy empinada, pues se vería así:
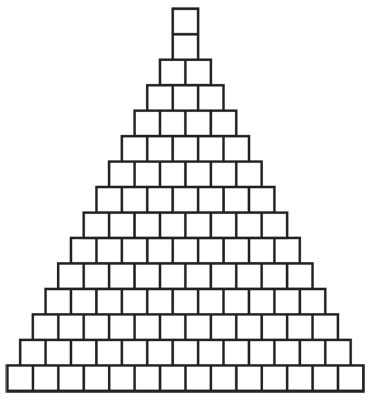
No olvidemos que el último nicho se añadió en la cima —el nicho que se quitó de 365 para obtener 364 = 4 · 91—. Para encontrar una solución mejor, quizá conviene no tratar de trabajar con ejemplos específicos sino con todos los ejemplos a la vez.
Las sucesiones aritméticas no siempre empiezan con el número 1 . Si se usa una variable, se puede decir que la sucesión empieza con a . Luego, en vez de aumentar por 1 , se puede decir que aumenta siempre en b , otra variable. Y se puede usar una tercera variable para denotar el número de niveles: n. La sucesión, entonces, empieza así:
a, a + b, a + b + b
donde el tercer número de nuestra sucesión es a + 2b, el cuarto es a + 3b, el quinto es a + 4b y el enésimo es a + (n − 1)b. La sucesión quedaría así:
a, a + b, a + 2b, a + 3b, a + 4b, . . . , a + (n − 2)b, a + (n − 1)b.
Con el argumento del joven Gauss, se puede calcular la suma de estos números y se obtiene la siguiente fórmula:
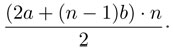
El problema consiste en encontrar números a, b y n tales que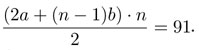 
. Si se multiplican ambos lados de esta ecuación por 2 se obtiene que:
(2a + (n − 1)b) · n = 182.
El lado izquierdo de esta ecuación es un producto y uno de sus factores es n. Por lo tanto el lado derecho debe ser divisible entre n. Como 182 = 2 · 91 = 2 · 7 · 13, se pueden probar diferentes opciones para el valor de n. Si se busca una pirámide con no demasiados niveles hay solamente una opción para asignar un valor a n y ésa es n = 7. Entonces n − 1 = 6 y se puede sustituir en la ecuación original, que queda así:
(2a + 6b) · 7 = 26 · 7.
Entonces 2a + 6b debe ser igual a 26. Nuevamente hay varias posibles soluciones —que son a = 1, b = 4; a = 4, b = 3; a = 7, b = 2 y a = 10, b = 1—, pero la que más se acerca a nuestro problema es a = 4 y b = 3. La sucesión que buscamos es:
4, 7, 10, 13, 16, 19, 22
y la pirámide tiene entonces la siguiente forma:
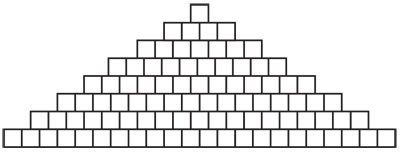
Es interesante comparar esta solución con la idea original de los totonacas antes de que hubieran añadido la rampa. La siguiente imagen muestra otro lado de la pidrámide que, además, es el mejor conservado.
Se observa sólo una diferencia con nuestra sucesión: el nivel superior tiene un nicho más. No sabemos cómo llegaron los totonacas a la solución, tal vez simplemente por ensayo y error, al intentar una y otra vez. El análisis que se llevó a cabo aquí requiere de ciertos conceptos y estrategias: necesita generalizar, atacar todas las opciones a la vez al usar variables. Esto es un proceso común en matemáticas. George Pólya, un matemático húngaro, decía que a veces es más fácil resolver muchos problemas en conjunto que uno solo a la vez porque al ver la generalidad se puede entender mejor. De esta manera es claro que la matemática ayuda a resolver problemas de nuestra cultura, algunos de importancia crucial, como en este caso.
