Un modelo matemático son una o varias fórmulas o ecuaciones, escritas en lenguaje matemático, que describen un proceso o un sistema de procesos. Los modelos matemáticos se usan para predecir o simular o, a veces, sólo para describir lo que pasa en la realidad. Hoy en día, todas las ciencias, incluso las sociales, modelan sus problemas con matemáticas. Por ejemplo, por medio de un modelo matemático se puede tratar de predecir cómo va a mutar un virus, cómo va a cambiar el clima en una región, se puede determinar la altura de un puente e incluso describir algún fenómeno económico y social.
Aquí presentamos un problema muy sencillo pero a la vez muy interesante: cómo medir la profundidad de un pozo. En realidad la idea fundamental no es que el lector entusiasmado vaya midiendo pozos por todos lados, sino que vea cómo, en principio, se hace un modelo matemático.
Para medir la profundidad de un pozo se pueden usar distintas estrategias. Una forma podría ser echar al pozo una cuerda con una piedra amarrada a un extremo. Después de oír que la piedra toca el agua, habría que sacar la cuerda y medirla. No parece ser un método muy práctico porque se necesita una cuerda muy larga. Además, el pozo puede ser profundo y oscuro, de manera que no es posible saber cuándo la cuerda llega al fondo.
Otra posibilidad es usar un cronómetro. Se puede medir el tiempo que transcurre entre que se deja caer la piedra y se escucha el sonido de la piedra al chocar en el agua. ¿Cómo se relaciona el tiempo que tarda la piedra en llegar al agua con la profundidad del pozo? En otras palabras, ¿cómo relacionar tiempo con distancia? Es claro que cuanto más tiempo transcurre, más profundo es el pozo, pero ¿cómo se puede obtener una medida de profundidad a partir de una medida de tiempo?
Cuando se suelta una piedra en un pozo, como sólo actúa sobre ella la fuerza de gravedad, decimos que cae en caída libre. La fórmula de caída libre es:
Por ejemplo, en una caída de 3 segundos (3 s), la fórmula nos daría una profundidad de:
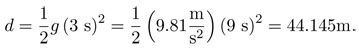
Es decir, un poco más de 44 metros. Éste es un primer modelo, el más sencillo, pero no el más exacto.
Como el pozo es oscuro, no se puede ver cuándo la piedra llega al fondo, solamente se escucha. Tomemos en cuenta, además, que el sonido tarda un cierto tiempo en llegar a nosotros; hay que buscar una manera de medir el tiempo que pasa desde que la piedra choca en el agua y el sonido sube por el pozo y llega a nosotros.
Como la velocidad del sonido (v ) es: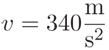 
, el tiempo que el sonido tarda en subir por el pozo puede calcularse con la fórmula:
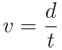
de la que puede despejarse la variable t:
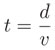
¡Cuidado! Aquí se ha vuelto a usar la variable t para denotar al tiempo, aunque ahora se trata de un tiempo diferente. En la caída, la variable t representaba el tiempo que tarda la piedra en caer y ahora representa el tiempo que tarda el sonido en subir desde el fondo hasta el escucha. Esto es algo que ocurre con frecuencia en matemáticas: el significado de una variable depende del contexto en el cual se usa. Para evitar confusiones, distinguiremos estos dos tiempos con un subíndice: tcaída para el tiempo de caída y tsonido para el del sonido.
Si el pozo realmente tuviera 44.1 metros de profundidad el sonido tardaría 0.13 segundos en recorrerlo. No es mucho, pero un segundo modelo del problema podría ser restarle este tiempo a los tres segundos que tardamos en escuchar la caída, lo que dejaría 3 − 0.13 = 2.87 segundos para la caída libre, lo cual resultaría en:
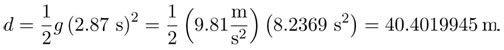
Esta segunda aproximación es más exacta, pero no del todo correcta, pues tomamos el tiempo del sonido para una profundidad que no es la que obtenemos. El problema radica en que no se conoce ni el tiempo de la caída ni el tiempo que tarda en subir el sonido por separado, lo único que se conoce es que el tiempo ( t ) desde que se suelta la piedra hasta que se escucha el golpe es la suma de ambos:
Las otras fórmulas importantes, que relacionan la distancia con los tiempos, son:
Lo que se busca es una fórmula que relacione la distancia d directamente con el tiempo total t . Para obtenerla se requiere cierta comodidad con el manejo del álgebra. El lector que no esté familiarizado con ella puede simplemente observar esto como un ejemplo particular. De la ecuación (1) se obtiene que:
tsonido = t − tcaída
Ahora se puede sustituir tsonido en la ecuación (3) por la expresión t − tcaída , lo que nos da una nueva ecuación:
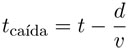
De esta ecuación se puede despejar la variable tcaída y se obtiene tcaída = 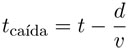. Sustituyendo lo anterior en la ecuación (2):
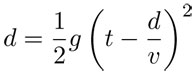
Ahora sí, obtuvimos una fórmula general y válida para cualquier pozo. Un tercer y último modelo para nuestro problema original que, admitimos, es una ecuación más complicada que la del primer modelo, donde únicamente se tomó en cuenta el tiempo de caída. Una ecuación compleja es un fenómeno común: entre mejor sea el modelo y más preciso, más complicadas serán las matemáticas involucradas. Así, tenemos que para un tiempo de t = 3 segundos se obtiene una profundidad d = 40.7 metros.
Resolvamos de postre otro problema relacionado con el anterior. Si en el pozo decidiéramos gritar, ¿cuánto tiempo pasaría hasta que se escuchara el eco desde el fondo del pozo?
Partamos de que, en cualquier pozo, el sonido tarda el mismo tiempo en bajar que en subir. Como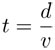 
, entonces el sonido tarda 
, donde d es la profundidad del pozo que equivale a d = 26.16942 metros y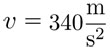 
es la velocidad del sonido en el aire.
Entonces,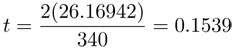
segundos. ¡Y ya acabamos!
