En 1920, David Hilbert propuso un ambicioso programa para subsanar los problemas de los cimientos de las matemáticas, que hoy se conoce, simplemente, como el programa de Hilbert.
Los puntos principales del programa de Hilbert eran:
Como veremos en esta sección, el programa de Hilbert fracasó: era demasiado ambicioso. No es que fracasara porque no hubiera suficientes esfuerzos vertidos en él, sino porque había obstáculos definitivos para lograrlo. Lo que Hilbert quería no se puede hacer, pero para comprenderlo más a fondo, es necesario entender mejor el primer punto: la formalización en sí.
Las matemáticas se escriben con símbolos que, en ocasiones, son muy raros. Por ejemplo, se suele usar el símbolo ∨ para la conjunción lógica "o". La cadena de símbolos p ∨ q expresa entonces "p o q", donde p y q son dos afirmaciones cualesquiera. En forma similar, se usa ∧ para expresar la conjunción "y", el símbolo ¬ para expresar "no". Por ejemplo:
(p ∧ q) ∨ ¬q (47)
quiere decir "se tiene p y q o se tiene no q". Esto tiene el mismo significado que "si p entonces q", que se suele escribir como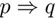 
. No se puede saber si 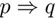es verdadero o falso, sin conocer la validez de p y q. Si p y q son verdaderos, entonces p ∧ q también es verdadero, mientras ¬q es falso. En consecuencia, 47 es verdadero.
La expresión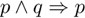 
siempre es verdadera, sin importar la validez de p y q. Por lo tanto, si sabemos que p ∧ q es verdadero, podemos sustituir esta expresión por p y obtenemos una nueva cadena que es verdadera. Similarmente, podemos sustituir p ∧ q por q ∧ p, es decir, 
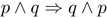es siempre verdadera.
Un sistema formal consiste en varias partes:
Un sistema lógico asigna valores de "verdadero" o "falso" a cada fórmula bien definida. Hagamos un ejemplo sencillo. El alfabeto es A = {1, +, =}. Una cadena de símbolos está bien formada si contiene exactamente un símbolo = y, además, cada símbolo + y cada símbolo = está encerrado entre dos símbolos 1. Por ejemplo:
111 + 11 + 1 = 111111 (48)
es una fórmula bien definida. Hay un único axioma que es 1 = 1. Las reglas de inferencia son las siguientes, las variables p, q, r, que aparecen son cadenas en los símbolos1, + tal que cada + está encerrado entre dos 1:
Si queremos podemos interpretar este sistema formal como el de la adición de números enteros positivos representados en el sistema unitario, es decir, simplemente indicando el número por la cantidad de símbolos 1. Habría que interpretar la ecuación (48) como 3 + 2 + 1 = 6. Con estas reglas de inferencia es posible deducir cualquier expresión matemáticamente correcta entre dos sumas o números enteros positivos. Las cadenas bien formadas que no se pueden deducir son falsas si las interpretamos en este sentido y las que sí se pueden deducir son verdaderas.
Del axioma 1 = 1 derivamos 111111 = 111111, al usar varias veces la segunda regla de inferencia. Con la primera regla de inferencia, p = 111 y q = 111 , obtenemos 111 + 111 = 111111 y, si la aplicamos nuevamente con , p = 111 + 11 y q = 1 , obtenemos 48. Formalmente, una demostración es una sucesión de fórmulas bien formadas, donde se indica en cada paso si es axioma o cómo se obtiene de una fórmula bien definida anterior. Nuestro ejemplo es sencillo, la demostración es:
