Si bien la balanza es una máquina creada por el hombre —que sirve para medir y comparar pesos—, su comportamiento depende de las leyes naturales al aprovechar la gravedad; dicho de otro modo, la balanza nos muestra cómo funciona la gravedad. Por lo anterior, al describir el funcionamiento de la balanza habremos descrito una pequeña parte de la naturaleza.
La balanza más sencilla es una tabla equilibrada sobre un rodillo, como se muestra en la figura 1.3.3.
Supongamos que la tabla y el rodillo son muy ligeros, pero firmes. La balanza mantiene
su estado de equilibrio si ponemos sobre la tabla dos pesas iguales a la misma distancia en ambos lados del rodillo, por ejemplo, de un kilogramo a un metro de distancia cada una:
Hay una ley que describe cómo cambia el peso al cambiar la distancia. Sabemos por nuestra experiencia que cuanto más lejos, menor peso se requiere. Esto es lo que nos dice la intuición, pero nos gustaría encontrar una ley precisa que nos diga qué peso, cuántos gramos habría que poner a dos metros del rodillo para equilibrar el peso de un kilogramo que está a un metro del rodillo. El siguiente razonamiento muestra que tiene que ser medio kilo. Podemos imaginarnos el kilogramo dividido en dos pesas iguales puestas sobre una balanza que, a su vez, reposa en el lugar en donde antes estaba la pesa de un kilo:
Como la balanza pequeña está en equilibrio podemos quitar el rodillo y la tabla de arriba —por hipótesis, su peso es despreciable— y apoyar las pesas directamente sobre la tabla grande sin que se altere el equilibrio. Finalmente, la pesa de medio kilo que se apoya justo sobre el rodillo central también puede quitarse.
Con ello descubrimos la ley básica de la balanza: al doble de distancia hay que poner la mitad del peso.
La ley general de la balanza se obtiene de este caso al usar consecutivamente el mismo procedimiento de sustituir las pesas por balanzas equilibradas. Por ejemplo, remplacemos ahora la pesa de un kilo del lado izquierdo por una nueva balanza equilibrada con pesas de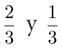 
de kilo, la primera colocada medio metro a la izquierda y la segunda un metro a la derecha del lugar que ocupaba la pesa de un kilo, como muestra la siguiente imagen:
Al volver a eliminar el rodillo y la tabla que sostiene a estas dos pesas, así como también la que queda sobre el rodillo de la balanza, obtenemos la siguiente balanza en equilibrio:
El lector atento se dará cuenta de que existe una ley detrás de estos números: si la distancia se duplica, el peso se divide a la mitad y si la distancia es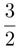 
de metro entonces el peso es de 
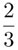, kilogramo. Podemos escribir esto como una igualdad:
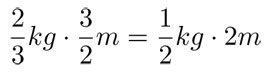
De esta manera podríamos argumentar para otros pesos y otras distancias. Y siempre encontraríamos que, cuando hay equilibrio, el producto del peso por la distancia al rodillo es igual en ambos lados. La fórmula matemática:
p1d1 = p2d2
expresa esta ley de manera muy sencilla: nos dice que el producto del primer peso p1 por su distancia d1, al rodillo, es igual al producto del segundo peso p2 multiplicado por su distancia d2 hasta el rodillo. En particular, la fórmula se satisface en el caso anterior pues:
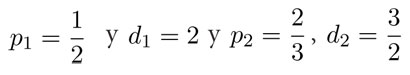
El lenguaje matemático es a la vez muy condensado y muy expresivo. En una sola fórmula se expresan todas las situaciones de equilibrio de una balanza. La fórmula cubre una infinidad de casos.
El ojo no entrenado no puede entender a primera vista la generalidad y la importancia de esta fórmula, al igual que el ojo de una persona no entrenada en la escritura musical no puede entender una partitura y el que no conoce las letras y sus combinaciones para un sistema lingüístico no puede entender algo escrito. Sin embargo, un poco de entrenamiento matemático permite comprender el significado de los símbolos que aparecen en la fórmula, la relación que expresa entre las cantidades representadas por los símbolos. Como queda claro, unas pocas matemáticas nos llevan muy lejos.
Además de la sencillez de la fórmula obtenida, resulta sorprendente que el razonamiento que nos llevó a descubrirla no requirió de experimentos con objetos reales. Fue suficiente hacerlos mentalmente y argumentar de manera lógica. No siempre es posible descubrir las leyes de la naturaleza por medio de experimentos mentales, sin embargo, estos últimos se utilizan muchas veces para acercarnos a ellas.
Mientras el caso de la esfera nos muestra un acercamiento directo a la naturaleza, el de la balanza nos revela una ley más profunda que se expresa mediante una fórmula matemática que llegamos a descubrir mediante razonamientos lógicos.
A continuación, presentaremos el caso de la gravedad que nos lleva a un tipo de fenómenos aún más complejos, en los que no basta la razón para descubrir las leyes naturales sino que hacen falta, además, experimentos que den información numérica que no podríamos obtener por pura lógica, pero en los que, las leyes que los rigen, siguen pudiéndose expresar con fórmulas matemáticas sencillas.
