En la sección anterior se llegó a una fórmula matemática para expresar una ley de la naturaleza: la de la balanza. Con ello queda ilustrado que las matemáticas pueden ser útiles para describir fenómenos naturales sencillos. Existen fenómenos mucho más complejos en los cuales las matemáticas no sólo son útiles sino verdaderamente imprescindibles. Uno de ellos es el de la gravedad. Comenzaremos por su aspecto más simple, la caída de los cuerpos.
Sabemos por nuestra experiencia diaria que los cuerpos caen. Si soltamos una taza ésta va a dar al suelo y probablemente se rompa. Desde épocas muy remotas se sabe lo anterior, pero no fue sino hasta 1590 cuando Galileo Galilei describió en términos matemáticos precisos el fenómeno de la caída libre —cuyo nombre expresa que nada se interpone en ella— de los cuerpos. Galileo demostró mediante la observación, la experimentación y el razonamiento que, cuando cae un cuerpo, su velocidad aumenta constantemente. Así, la velocidad del cuerpo que cae es proporcional al tiempo que ha transcurrido desde que comenzó a caer. La constante de proporcionalidad se llama la aceleración de la gravedad, se denota por g, y hoy sabemos que su valor es de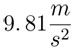 
. Esto quiere decir que la velocidad de un cuerpo en caída libre aumenta en 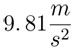cada segundo. En fórmula, lo anterior se escribe así:
v = gt
donde v es la velocidad del cuerpo, t es el tiempo transcurrido desde que comenzó su caída y g es la constante de la aceleración de la gravedad.
Galileo demostró que, como consecuencia de esta ley de movimiento según la cual la velocidad aumenta constantemente con el tiempo, la distancia recorrida por el cuerpo en su caída aumenta de manera cuadrática con respecto al tiempo, es decir:
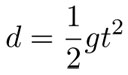
donde d es la distancia que un cuerpo ha recorrido en su caída, t es el tiempo que ha transcurrido desde que comenzó a caer y g es la constante de la aceleración de la gravedad.
El siguiente esquema muestra una pelota que cae de un edificio de 80 metros y una gráfica con las posiciones de la pelota cada dos décimas de segundo.
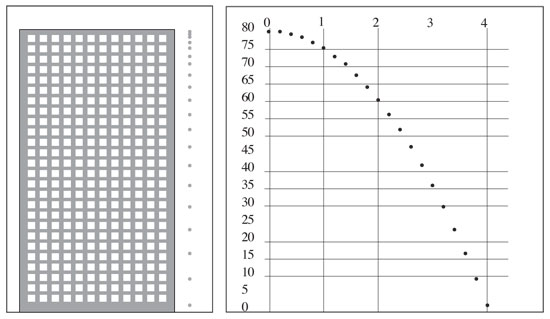
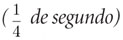. A la derecha, se observa la gráfica de la altura contra el tiempo.
La forma que une los puntos de la gráfica es una curva conocida ya por los antiguos griegos a la que llamaron parábola. En la gráfica se observa que la pelota cae aproximadamente 5 metros durante el primer segundo, el triple de 5 durante el siguiente segundo, cinco veces esa misma cantidad durante el tercer segundo y siete veces la cantidad durante el cuarto segundo. Es decir, la distancia recorrida sigue la sucesión 1, 3, 5, 7 . . . de los números impares. Por tanto, la distancia total que ha caído en cada segundo es la suma de los primeros impares: 1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7 . . . que son los cuadrados de los números enteros 1, 4, 9, 16,, etc. Esta observación podemos escribirla como:
d = 4.9 · t2
que corresponde a la fórmula de Galileo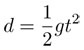 
ya que 
.
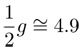Por ejemplo, la distancia que recorre un cuerpo en caída libre en el doble de un lapso de tiempo es cuatro veces la que recorrió en el lapso original. La distancia recorrida en el triple de un lapso de tiempo es igual a nueve veces la distancia original. Esta fórmula representa la ley del movimiento de caída libre. No es una ley lineal sino cuadrática: la velocidad depende linealmente del tiempo, pero la distancia recorrida es proporcional al cuadrado del tiempo.
No es una ley complicada, pero podríamos considerar que es ligeramente más compleja que la que describe a la balanza, pues en aquélla no aparecen cantidades elevadas al cuadrado y en ésta sí.
Galileo demostró también que la trayectoria descrita por un objeto lanzado al aire es una parábola, esa curva que habían estudiado dos mil años antes los griegos por razones enteramente diferentes; de hecho, la usaron para intentar resolver el problema —meramente matemático— de la duplicación del cubo, que consistía en encontrar el lado de un cubo que tuviera el doble del volumen de otro cubo dado.
Si regresamos a la parábola como trayectoria de una piedra o bala lanzada, lo sorprendente es que Galilei obtuvo esta descripción no de la observación directa sino mediante una argumentación lógica. Para ello tuvo que introducir la relatividad del movimiento. Su ejemplo es famoso: si dejamos caer una piedra desde una torre, ésta cae por una trayectoria vertical al piso. Pero si dejamos caer la piedra desde un mástil de un barco que navega en una dirección, ¿dónde caerá la piedra?, ¿junto al mástil o detrás de éste porque cae de forma vertical y mientras tanto el barco avanza? El hecho es que cae junto al mástil. La explicación de Galileo es que el marinero que deja caer la piedra cree que cae vertical porque él también se mueve, pero para un espectador en la playa la piedra no sólo cae, sino que al soltarla se impulsa en la dirección del barco. De esta manera, Galileo descubre que las velocidades pueden descomponerse en una componente vertical y otra horizontal.
El movimiento de caída libre no parecía tener nada que ver con el movimiento de los planetas, hasta que uno de los más grandes genios de la historia de la ciencia, Isaac Newton, pensó en relacionarlos. El resultado de esas investigaciones constituye uno de los mayores logros científicos, quizá la hazaña intelectual más importante de todos los tiempos. Lo más sorprendente es que está al alcance de cualquier estudiante de bachillerato dispuesto a familiarizarse con la manipulación de algunas expresiones algebraicas no muy complicadas. Para acercarnos al tema es necesario que repasemos los conocimientos que la humanidad tenía del movimiento planetario en la época de Newton.
Johannes Kepler fue un contemporáneo de Galileo que dedicó la mayor parte de su vida al estudio de las órbitas de los planetas, es decir, a las trayectorias que describen los planetas alrededor del Sol. Kepler era un hombre profundamente religioso y convencido de que Dios dispuso a los planetas en perfecta armonía describiendo figuras geométricas sencillas. Gracias a las mediciones precisas de Tycho Brahe, después de muchos intentos fallidos con circunferencias y óvalos, le fue posible describir las órbitas celestes mediante la elipse, curva que al igual que la parábola había sido estudiada por los griegos por sus propiedades puramente geométricas. Kepler formuló sus hallazgos principalmente en dos de sus libros: Astronomia nova (Nueva astronomía, 1609) y Harmonices mundi (La armonía de los mundos, 1619) en los que describe el movimiento de los planetas en tres leyes, llamadas las leyes de Kepler del movimiento planetario.
1. Los planetas giran alrededor del Sol como órbitas elípticas, donde el Sol es uno de los focos.
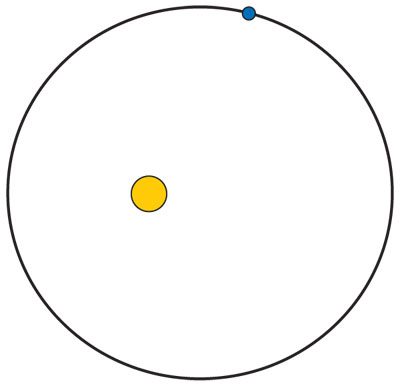
2. Los radios-vectores de los planetas respecto al Sol barren áreas iguales en tiempos iguales.
3. Los cuadrados de los periodos de revolución de los planetas son proporcionales a los cubos de los radios medios de sus órbitas.
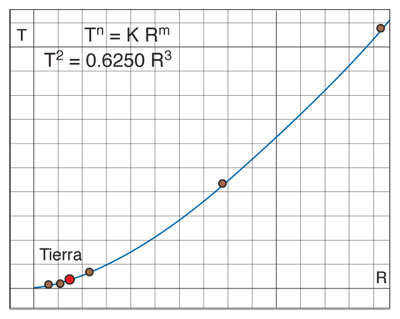
Conviene hacer algunas aclaraciones sobre estas leyes. La primera, aunque afirma que las órbitas de los planetas son elípticas, en realidad se trata de elipses con una excentricidad muy pequeña, lo que quiere decir que son casi circulares. La segunda nos indica que los planetas se mueven con mayor velocidad cuando están más cerca del Sol que cuando están más lejos. Finalmente, la tercera, que puede resultar muy extraña, no es más que el descubrimiento de que los radios de las órbitas y sus tiempos de revolución no son arbitrarios, sino que guardan una relación funcional que no es lineal ni cuadrática, más bien algo intermedio: el cuadrado del tiempo es proporcional al cubo del radio:
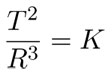
donde K es un número fijo para todo el sistema planetario, el mismo para todos los planetas.
Es importante observar que la tercera ley le llevó a Kepler doce años más que las otras para descubrirla y representa una relación muy precisa entre la velocidad con la que giran los planetas y sus distancias al Sol. ¿Cómo es que se da esta relación aparentemente tan extraña? No hay ninguna relación aparente entre los radios de las órbitas y, por ejemplo, los tamaños de los planetas. ¿Qué hace que sí la haya entre los periodos y los radios? ¿Y por qué es a la vez tan simple y tan extraña?
Kepler propuso un modelo matemático del movimiento de los planetas pero no una explicación. Creía que estas leyes provenían de la mano de Dios y no requerían mayor comprensión.
Así quedaron las cosas por varios años hasta que, en 1687, se publicó el libro Philosophiae Naturalis Principia Mathematica de Isaac Newton, matemático, físico y astrónomo inglés. En este libro, Newton explica que se pueden deducir las tres leyes de Kepler a partir de leyes más fundamentales y simples.
La idea principal de Newton es que debe haber una fuerza que mantiene a los planetas en órbitas alrededor del Sol y esa misma fuerza debe ser la responsable del movimiento de caída libre de los cuerpos sobre la Tierra.
Antes de llegar a esta idea Newton, al continuar el trabajo de Galileo, había establecido sus tres famosas leyes:
1] Todo cuerpo permanece en estado de reposo o de movimiento rectilíneo uniforme a menos que haya una fuerza externa que lo modifique.
2] Cuando una fuerza actúa sobre un cuerpo, éste adquiere una aceleración constante proporcional a la magnitud de la fuerza e inversamente proporcional a la masa del cuerpo.
3] A toda acción corresponde una reacción igual y en sentido contrario.
En símbolos, la segunda ley de Newton se escribe así:
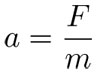
donde a es la aceleración que recibe el cuerpo, m es su masa y F es la fuerza que actúa sobre él. Para Newton era claro que si los cuerpos caen es debido a que hay una fuerza que los atrae hacia el suelo y esta fuerza debe ser proporcional a la masa del cuerpo ya que todos los cuerpos, independientemente de su masa, caen con la misma aceleración g. La Tierra atrae a los cuerpos sobre su superficie con una fuerza F = mg, donde m es la masa del cuerpo, aunque en forma coloquial decimos "el peso" del cuerpo. Con este razonamiento, Newton define el concepto de la masa de un cuerpo y lo relaciona con su peso por medio de la constante g; a la vez, diferencia ambos conceptos al definir a la masa como una propiedad intrínseca del cuerpo, mientras que considera al peso como una propiedad del cuerpo en relación con la Tierra, es decir, representa la fuerza con la que la Tierra lo atrae.
Al razonar con ayuda de la simetría y apoyado en su tercera ley del movimiento, Newton piensa que si la Tierra atrae a los cuerpos que se encuentran cerca de su superficie con una fuerza proporcional a la masa de los mismos, entonces debe haber otra fuerza, igual y en sentido contrario, con la que cada cuerpo atrae a la Tierra y esta fuerza, lógicamente, también debe ser proporcional a la masa de la Tierra. Dicha fuerza debe ser la responsable de la caída de los cuerpos hacia la Tierra y también de las trayectorias de los planetas que, en lugar de ser líneas rectas, giran alrededor del Sol porque éste los atrae. Ésta es la gran idea de Newton: hay una fuerza de atracción entre todos los cuerpos, que aumenta proporcionalmente con la masa de cada cuerpo.
A partir de las ideas anteriores y por deducción matemática, Newton logró establecer que la fuerza de atracción entre dos cuerpos de masas m y M que se encuentran a una distancia R debe tener la forma:
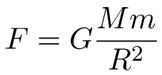
donde G es una constante universal, es decir, es la misma para todos los cuerpos. Ésta es la famosa ley de la gravitación universal de Newton. Dice que la fuerza de gravedad con la que se atraen dos cuerpos de masas M y m es proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia R que los separa. G se llama la constante de la gravitación universal y puede calcularse a partir de la aceleración de la gravedad g y el radio r y la masa m de la Tierra. Esta fórmula expresa una ley de la naturaleza de manera compacta y precisa. Las matemáticas son enormemente económicas: con sólo ocho símbolos —cinco letras, un número, una igualdad y una raya de quebrados— se expresa todo este profundo conocimiento. Al final de esta sección hay una deducción de esta fórmula a partir de la tercera ley de Kepler.
Newton logró demostrar que las tres leyes del movimiento planetario de Kepler son meras consecuencias matemáticas de la ley de la gravitación universal y de sus tres leyes básicas del movimiento de los cuerpos. Este hecho constituye una explicación científica completa del movimiento planetario. Una ley universal que explica los movimientos de todos los cuerpos terrestres y celestes de manera unificada y clara. Probablemente no hay otro descubrimiento científico de mayor trascendencia y belleza que éste. El lector interesado en estas deducciones podrá seguirlas en el tema 3, en la sección sobre "Espacio, tiempo y movimiento".
Para llegar al descubrimiento de la ley de la gravitación universal, Galileo, Kepler, Newton y muchos científicos más tuvieron que luchar contra las ideas preconcebidas que imperaban en aquella época, algunas de carácter religioso y otras apoyadas en antiguas tradiciones, pero todas haciendo una apología irracional de la ignorancia y la intolerancia. A nosotros, seres humanos del siglo XXI, nos parece natural que una misma ley de la naturaleza explique fenómenos terrestres y celestes, pero debemos recordar que en aquel entonces se pensaba que lo que pasaba en la Tierra era algo de naturaleza muy distinta a lo que pasaba en el cielo, el cual se identificaba no con lo material sino con lo divino. Según Aristóteles, el cielo y sus ingredientes como el Sol, la Luna, las estrellas y los planetas, estaban compuestos por una materia completamente distinta a las terrenales. Las ideas de Galileo, Kepler y Newton fueron por tanto muy revolucionarias: la atracción de la gravedad actúa de la misma manera en el cielo y en la Tierra. La misma ley explica, por un lado, el movimiento de los planetas alrededor del Sol, el de la Luna alrededor de la Tierra y la caída de los cuerpos sobre la superficie terrestre y predice que, en cualquier astro celeste, debe haber una fuerza que hace caer a los cuerpos que se encuentran sobre su superficie. La atracción gravitatoria actúa en la Tierra y en el cielo, en el sistema solar y entre estrellas y galaxias, siempre de la misma manera.
Parece haber una relación muy íntima entre la naturaleza y las matemáticas, tal como Galileo Galilei lo hiciera notar en la nota que aparece al principio de esta sección y que escribió muchos años antes del descubrimiento de Newton. Quizá esa idea suya inspiró a Newton e inspira a los científicos, cuya misión es estudiar a la naturaleza al tratar de descubrir sus leyes y expresarlas, de preferencia, en lenguaje matemático, porque cuando esto se logra se obtiene un conocimiento que es a la vez profundo y sencillo.
Ésta es una de las grandes fuerzas inspiradoras y generadoras de las matemáticas.
Como la ley de la gravitación universal es uno de los grandes logros culturales, en este primer capítulo quisimos explicar la deducción de la fórmula —a pesar de que el álgebra requerida para ello rebasa el nivel de las matemáticas usadas hasta ahora— que se encuentra en el recuadro a continuación. Ya se mencionó que en los libros de matemáticas hay partes más difíciles de leer; ésta es una de ellas y, por consiguiente, se puede omitir, si el lector siente que no entiende, para reanudar la lectura a partir de la siguiente sección.
