Volviendo a la antigua Grecia, la experiencia de haber descubierto que se pueden obtener resultados generales con demostraciones formales, como el teorema de Pitágoras, dio un impulso enorme a las matemáticas. Se puede decir que con ello se da su banderazo de salida. La recién creada "escuela pitagórica" plantea muchos problemas y avanza en la sistematización de las matemáticas. Para sus miembros, fue como descubrir un continente inexplorado con tesoros y recompensas detrás de cada loma: teoremas y más teoremas, demostraciones y construcciones. Los hizo sentir que habían encontrado el camino del entendimiento y la iluminación por medio de la razón; experimentaban colectivamente el éxtasis de la creatividad intelectual y se constituyeron como una secta. Los pitagóricos llegaron a creer que la estructura del Universo era aritmética y geométrica. Y lo creyeron con tal fervor que, cuando un joven de su escuela demostró con sus propios métodos que había una distancia que no se podía expresar mediante números, tomaron una actitud sobrecogedora que revela lo profundo de su convicción. Decidieron que se trataba de un error de Dios y que, como escuela, tenían la obligación de guardarle el secreto. Juraron sobre su vida no revelar nunca ese desliz en la "creación" del Universo.
El argumento del joven que reveló el "fallo de las divinidades" se conoce ahora como el descubrimiento de los números irracionales o, más concretamente, de que la raíz cuadrada de dos es irracional. La concepción que tenían los pitagóricos de la "aritmética" es que los números se expresan como razón entre dos naturales, que son de la forma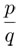 
con p y q enteros; éstos son lo que ahora conocemos como números racionales, porque se expresan como una "razón", a pesar de que en México les llamamos "quebrados". Por otro lado, en la geometría surge de manera muy natural una longitud, la de la diagonal de un cuadrado unitario, con lado 1.
Como dicha diagonal es la hipotenusa de un triángulo rectángulo con catetos de longitud 1, por el teorema de Pitágoras, al elevar a este número al cuadrado se obtiene 2, pues 12 + 12 = 1 + 1 = 2 . A este número lo llamamos ahora "raíz de 2" y lo denotamos √2 . Para los griegos era el lado de un cuadrado con área 2. Suponer que √2 se expresa como quebrado o fracción lleva a una contradicción —lo que los pitagóricos explicaron como "un error de Dios"—. Veamos cómo llegaron a esa contradicción.
Si suponemos que √2 es una fracción, entonces deberían existir dos números enteros p y q , tales que:
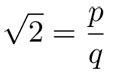
Puede considerarse que p y q no son ambos pares —cada quebrado se puede escribir así, ya que las fracciones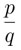 
pueden simplificarse hasta que el numerador o el denominador no sea par; por ejemplo, cuando simplificamos 
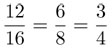, el numerador ya no es par. Al multiplicar ambos lados de la igualdad anterior por q se obtiene la nueva igualdad:
Si ahora se elevan al cuadrado ambos miembros, como (√2 · q)2 = 2 · q2, se observa que:
2 · q2 = p2.
Como el lado izquierdo es par, ya que 2 es uno de sus factores, también lo es el lado derecho, es decir, p2 es un número par. Obsérvese que el cuadrado de un número impar siempre es impar y que el cuadrado de un número par, además de ser par es divisible por 4 . Así que como p2 es par, debe ser divisible por 4. Por tanto, se sigue que q2 también es par y, entonces, también q es par. Esto contradice lo que supusimos sobre p y q al principio de nuestro argumento: que no eran ambos pares. Esta contradicción nos indica que la hipótesis de que √2 podía escribirse como una fracción, como un quebrado, tiene que ser falsa. En otras palabras, √2 no puede ser un número racional y, por definición, es irracional.
De las propias matemáticas, de la interacción de dos de sus disciplinas —la aritmética y la geometría— y con razonamientos matemáticos, surgió un descubrimiento inesperado. Y con él, una andanada de preguntas y problemas: ¿habrá más números irracionales?, ¿cómo los expresamos o trabajamos con ellos?, etc. Éste es otro ejemplo histórico de cómo las matemáticas se motivan a sí mismas para crecer e indagar continuamente.
Por último, veamos un ejemplo de cómo algunos desarrollos matemáticos tienen consecuencias inesperadas y profundas tanto en la comprensión de la naturaleza como en la actividad humana.
El ímpetu que se dio al desarrollo de las matemáticas en la antigua Grecia alcanza un clímax con la aparición, alrededor del año 300 a.C., de Los elementos de Euclides. Son una serie de libros en los que se sistematizan los resultados y los conocimientos de geometría que se habían obtenido hasta ese momento, y en los que se establece el método axiomático. Nuestras ideas abstractas de punto, línea, plano, distancia, ángulo, área, volumen, etc., se fundamentan en esa obra, que se usó como libro de texto por más de dos milenios. En ella, se delinea el modelo teórico de lo que subyace al espacio en que vivimos, que se llama aún el espacio euclidiano y es el escenario de la geometría de nuestro entorno. Suponemos desde entonces que sobre un espacio euclidiano —la esencia geométrica tridimensional mínima, limpia y vacía— está transcurriendo el mundo y que ahí se hospeda y se mueve la materia, el mundo físico con nosotros incluidos. Y esto sigue siendo válido sólo en pequeña escala, porque Einstein, a principios del siglo XX, nos cambió esa idea a gran escala. Pero, en fin, en el espacio euclidiano es donde tiene sentido hablar de planos, y en ellos de triángulos y de círculos.
Emparentadas íntimamente con los círculos están las elipses. Un círculo visto de lado es una elipse; de alguna manera, las elipses son círculos "apachurrados". En muchos casos en los que nuestros ojos ven una elipse —vasos, tazas, llantas, etc. —, nuestra mente lo interpreta como un círculo porque el cerebro "sabe" que al cambiar el punto de vista la figura es, efectivamente, un círculo. Los griegos se dieron a la tarea de estudiarlas y, en particular, de dar una definición precisa de ellas. Encontraron dos. La primera tiene que ver con cómo trazarlas en el plano. Son el lugar geométrico de los puntos cuya suma de sus distancias a dos puntos fijos, llamados focos, es constante. Así que para trazar una elipse en un jardín tendríamos que hacer lo siguiente: se clavan dos estacas —que serían los focos—, se les amarra una cuerda holgada cuya longitud es la constante que se menciona en la definición y, luego, al ir tensándola en todas las direcciones, se dibuja la elipse. A partir de esta definición queda claro que el círculo es un caso límite de elipse que corresponde a cuando los dos focos coinciden en su centro y, entonces, la constante es el doble del radio.
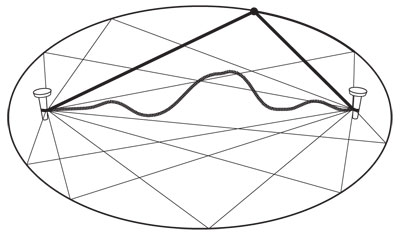
La segunda definición tiene que ver con la percepción de círculos y necesita de la tercera dimensión pues se sale del plano. Si levantamos el centro de un círculo perpendicularmente al plano en el que "vive" —digamos que horizontal— y luego consideramos todas las líneas que van de este punto al círculo, obtenemos un cono circular. Las elipses se obtienen al cortar este cono con planos inclinados cercanos al horizontal —la dirección en la que se inclina el plano, corresponde a aquella en la que se "alarga" el círculo. Nuestra percepción de círculos se explica con el proceso inverso: un cono elíptico cortado por otro plano origina el "círculo" real.
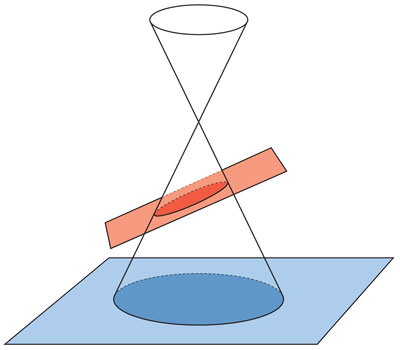
Si inclinamos más de la cuenta el plano —y ya que estamos en la teoría, no hay nada que nos detenga, por lo que sería natural hacerlo—, se obtienen dos nuevos tipos de curvas: las parábolas y las hipérbolas. De aquí el nombre de secciones cónicas que dieron los griegos, con la participación destacada de Apolonio de Perga, a estos tres tipos de curvas planas. Obtuvieron descripciones de estas curvas como lugares geométricos en términos de distancias, similares a la que vimos para las elipses. Se maravillaron con los resultados que obtuvieron y que dejaron como legado a la posteridad. Hicieron matemáticas por sí mismas que parecían muy alejadas de la "realidad".
Quién hubiera pensado en ese entonces que, dos milenios después, esas mismas curvas sirvieran para entender fenómenos físicos como la trayectoria de los planetas alrededor del Sol —que son elipses con el Sol en uno de sus focos—, o las trayectorias de las balas o proyectiles —que describen parábolas. O bien, dentro de las propias matemáticas, como cuando Descartes puso coordenadas al plano y las secciones cónicas reaparecen como soluciones de ecuaciones cuadráticas con dos incógnitas. O, más aún, que las hipérbolas serían fundamentales para diseñar los lentes ópticos y las parábolas para las telecomunicaciones del presente. Esa "magia" que se ha dado una y otra vez en la historia, ese hecho insólito de que las matemáticas desarrolladas por sí mismas luego reaparecen y se interconectan con otros fenómenos al parecer independientes —tanto de la naturaleza como de la actividad humana—, es uno de sus grandes misterios. Hace pensar, como lo harían Pitágoras, Platón y luego Galileo, que son la herramienta fundamental para entender nuestro entorno.
