
El principio del siglo XVII es el tiempo de Galilei, de la aceptación del método científico, el tiempo de Tycho Brahe y de Kepler, de los telescopios que permitían una observación más precisa de la bóveda celeste y el tiempo de Blaise Pascal, quien elaboró una de las primeras máquinas que podían sumar y multiplicar. En aquel entonces también aparecen innovaciones importantes al elaborar los relojes de precisión. En resumen, la primera mitad del siglo XVII es una era donde la mecánica fina se vuelve importante para la ciencia y la sociedad.
Sin embargo, la mecánica fina requería también unos cálculos cada vez más precisos. Fue a inicios del siglo XVII cuando Jost Bürgi —matemático y relojero suizo— descubrió los logaritmos al intentar facilitar su trabajo con los cálculos de precisión —que eran bastante tediosos en aquel entonces—, también descubiertos y publicados por John Napier, una década después. Hay muchas historias parecidas en las que se habla de que el tiempo es "maduro" para cierto descubrimiento pues, simultáneamente, varias personas encuentran lo mismo de manera independiente. Hoy en día el mundo reconoce a Napier como el descubridor de los logaritmos y, tal vez, ello sea correcto dado que fue él quien divulgó la idea y, así, la puso al servicio de la humanidad.
A continuación veremos en qué consisten estos logaritmos y por qué son tan útiles para facilitar el trabajo con los cálculos. Empezaremos como lo hicieron Bürgi y Napier, al considerar sucesiones algebraicas y geométricas, que se muestran respectivamente a continuación:
2, 5, 8, 11, 14, . . .
3, 9, 27, 81, . . .
Aquellos que gusten de los retos intelectuales se pueden preguntar cómo sigue cada una de estas sucesiones, es decir, ¿cuál es el siguiente número? Para ello hay que indagar sobre el patrón que rige la sucesión. En nuestro caso no es difícil: en la primera, el aumento de un número a otro es siempre el mismo y cada vez la sucesión crece en tres unidades, mientras que, en la segunda, cada nuevo número se obtiene al multiplicar el anterior por 3.
Veamos la segunda sucesión más de cerca: empieza con 3 y luego este 3 se multiplica repetidamente por 3. Podemos escribir la sucesión de la siguiente manera:
3, 32, 33, 34,
En este caso, la simple observación que da lugar al descubrimiento de Bürgi y Napier es el constatar que la sucesión de los exponentes:
1, 2, 3, 4, . . .
es una sucesión algebraica. El gran problema de los cálculos en aquella época no fue la suma, sino la multiplicación. ¿Cómo multiplicar 35 con 37 ? Consideremos que 35 = 243 y 37 = 2187. Ahora, podríamos calcular el producto, pero puede ser provechoso observar que 35 es el producto de cinco 3, y 37 el producto de siete, por lo que:
35 · 37 = 35+7 = 312.
Hasta aquí parece que no hemos ganado nada, sólo hicimos una adición, sumamos los exponentes. Ahora bien, si pudiéramos representar más números como potencias del 3 podríamos rápidamente hacer más multiplicaciones al efectuar una única suma.
En efecto, lo anterior se hizo pero no con el número base 3 sino con el 10, dado que
nuestro sistema es decimal. Aquí se muestran algunos valores:
1 = 100
2 = 100.301
3 = 100.477
4 = 100.602
5 = 100.699
6 = 100.778
7 = 100.845
8 = 100.903
9 = 100.954
10 = 101
Así, por ejemplo, 2 · 3 = 100.301· 100.477 = 100.301+0.477 = 100.778 = 6. ¡Claro! Sabemos multiplicar 2 por 3 más velozmente en nuestra cabeza, pero este simple ejercicio explica el funcionamiento.
En aquel tiempo se empezaron a elaborar libros enteros que contenían tablas de logaritmos, como se muestra en la figura 2.14.
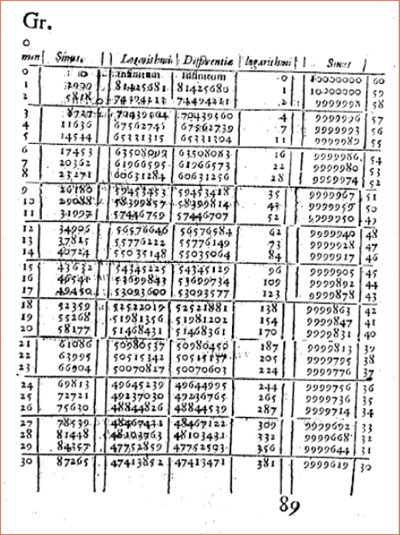
Elevar al cuadrado significa duplicar el exponente: lo vemos si comparamos los exponentes que corresponden a los números 2, 4 y 8 , que respectivamente son 0.301, 0.602 y 0.903. De manera similar, obtener la raíz de 5 es ahora fácil: hay que dividir el exponente correspondiente entre 2, lo que es lo mismo que:
√5 = 10.699÷2 = 100.3495.
Con una tabla de logaritmos se puede buscar rápidamente el valor, que es 2.236. Para multiplicar 61.235 por 5.961 se buscan los exponentes correspondientes que son, precisamente, los logaritmos de dichos números en la tabla. Entonces, se encuentra log 61.235 = 1.787 —que equivale a decir que 61.235 = 101.787— y log 5.961 = 0.775.
Por lo tanto, su producto satisface que:
log(61.235 · 5.961) = 1.787 + 0.775
y obtenemos un cálculo sencillo que se puede hacer casi en la cabeza, cuyo resultado es 2.562 .
Buscando en las tablas de logaritmos se encuentra que 102.562 = 364.8, lo cual se acerca bastante bien al resultado correcto, que es 61.235 · 5.961 = 365.021835. Para tener mayor precisión, se requerían libros cada vez más gruesos con tablas de logaritmos más precisos.
Ya en 1624, Henry Briggs publicó la primera tabla donde reportó los logaritmos de los primeros 20 mil números naturales con una precisión de 14 dígitos decimales. A finales del siglo XVII, se publicaron varios libros con logaritmos en los que se calculaba hasta con 6 dígitos de precisión.
La regla de cálculo que se muestra en la figura 2.13 fue inventada poco después del descubrimiento de los logaritmos. El principio se basa en que ambos lados muestran escalas logarítmicas. Así, con un simple deslizamiento, se podía leer directamente el resultado de una multiplicación hasta, al menos, con un dígito de precisión sin tener que hacer cálculo alguno.
La regla de cálculo desapareció rápidamente con la aparición de las calculadoras de bolsillo, que usan en su arquitectura binaria el principio de los logaritmos y lo combinan con rutinas eficientes para calcular tanto los logaritmos como sus inversos, los exponenciales, para no almacenar tablas grandes de información.
El ejemplo de los logaritmos muestra uno de los grandes logros en el que se aprecia cómo la humanidad usa las matemáticas para simplificar el quehacer de calcular. Al mismo tiempo, muestra que todos estos descubrimientos e inventos están presentes en nuestra cultura de manera oculta, en este caso, en las calculadoras de bolsillo.