A principios del siglo XIX no se sabía cuál era la montaña más alta del planeta ni se conocía el tamaño de la Tierra con precisión. La medida conocida como metro la establecieron los franceses con la idea de que fuera la 10 000 -ésima parte de la distancia del Ecuador al Polo Norte. Casi al mismo tiempo, los ingleses iniciaron el Great Trigonometrical Survey —gran proyecto de topografía trigonométrica— para medir con precisión toda la India, colonia británica en aquel entonces, pues se pretendía tener una visión más realista del territorio que ocupaba el Imperio británico en Asia y, a la vez, tener una medida más precisa del tamaño de la Tierra. Este proyecto consumió grandes recursos, duró casi todo el siglo XIX y permitió establecer la altura del monte Everest, nombrado así en honor al coronel que estuvo a cargo del proyecto —aunque finalmente ya no vio la montaña pues se quedó ciego—. Fue hasta ese momento que se supo que el Everest, a 8 850 metros sobre el nivel del mar, era más alto que los Andes.
En esta sección veremos los principios básicos del proceso para medir la superficie terrestre conocido como "triangulación" —basado en la medición y el cálculo de triángulos, por ejemplo, entre tres picos de montañas. Claro que estos triángulos, en general, no serán ni rectángulos —que tienen un ángulo de 90°— ni isósceles —con dos o tres lados iguales—, sino que son triángulos arbitrarios. Para aclarar la relación que existe entre los lados y los ángulos, tenemos que empezar primero con triángulos rectángulos.
En un triángulo rectángulo, a los dos lados que forman el ángulo recto se les llama catetos, y al lado opuesto, hipotenusa. Los ángulos de un triángulo rectángulo quedan determinados por cualquiera de sus ángulos no rectos, pues entonces, la medida del otro ángulo corresponde a lo que falta para 90° —recordemos que los tres ángulos internos de un triángulo suman 180°—. Si elegimos uno de los ángulos no rectos y lo llamamos α, podemos diferenciar a los dos catetos. Al lado que forma α con la hipotenusa, se le llama cateto adyacente y se le denota CA; al lado opuesto al ángulo α , cateto opuesto y se le denota CO y, finalmente, a la hipotenusa con H.
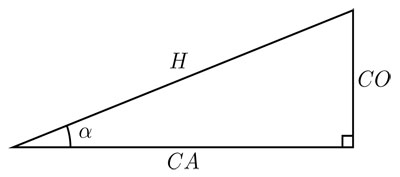
Las funciones trigonométricas son las proporciones entre los lados de los triángulos rectángulos. Las básicas son el coseno y el seno, definidas como:
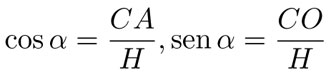
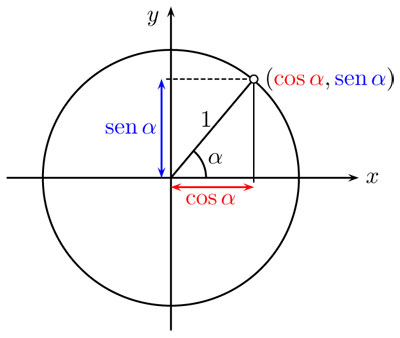
Observemos que cuando la hipotenusa mide 1 —que es igual a decir que H = 1—, el coseno y el seno son, precisamente, lo que miden los catetos. Así, podemos pensar que son las coordenadas cartesianas de un punto en el círculo unitario, es decir, el círculo de radio 1 con centro en el origen. En esta manera de ver al coseno y al seno, los puntos del círculo unitario quedan parametrizados por el ángulo con el eje de las x, como se muestra en la figura 2.24.
Al pensar en el seno y el coseno como coordenadas es natural extender su definición a cualquier ángulo con los signos correspondientes a los de los cuatro cuadrantes.
Planteemos ahora un problema más complicado: medir la altura de una montaña sin subir en ella. No podemos usar triángulos rectángulos pues no podemos acceder al interior de la montaña, pero sí se pueden hacer mediciones suficientes desde afuera para determinar un triángulo del que se conozcan dos de sus ángulos y un lado. Luego, utilizando la llamada ley de los senos, que veremos a continuación, se pueden calcular los otros dos lados.
En un triángulo cualquiera, tracemos una de sus alturas y llamémosla h; a los ángulos opuestos a ella, denotémoslos α y β, mientras que los lados opuestos —en el triángulo original—, serán a y b, respectivamente.
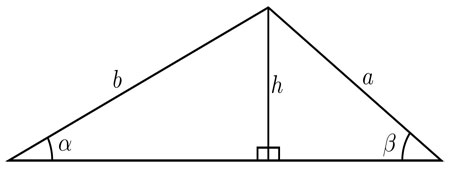
El seno de α se puede expresar como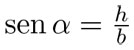 
de donde podemos despejar h:
h = b sen α.
De manera análoga, obtenemos que h = a sen β. Hemos descrito a h de dos maneras diferentes, lo que nos da la igualdad: b sen α = a sen β, que también se puede escribir como:
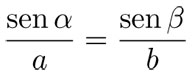
Esta ecuación es el principio básico de la ley de los senos, aunque la manera más común de presentarla es igualando los inversos e incluyendo al tercer ángulo γ y a su lado opuesto, c. Para hacerlo, hay que realizar el mismo razonamiento con alguna de las otras dos alturas. De tal manera, para cualquier triángulo se cumple el que la proporción de los lados con respecto a los senos de sus ángulos opuestos sea la misma. Al expresar la ley de los senos en forma de ecuaciones tendríamos:
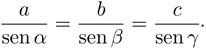
Regresemos ahora al problema de la montaña para aplicar la ley de los senos. Llamemos C a un punto del pico visible. Desde dos puntos A y B en la falda, se pueden medir los ángulos correspondientes α y β triángulo ΔABC . Supongamos que también conocemos la distancia c entre A y B.
Por la ley de los senos, se obtienen las distancias a y b:
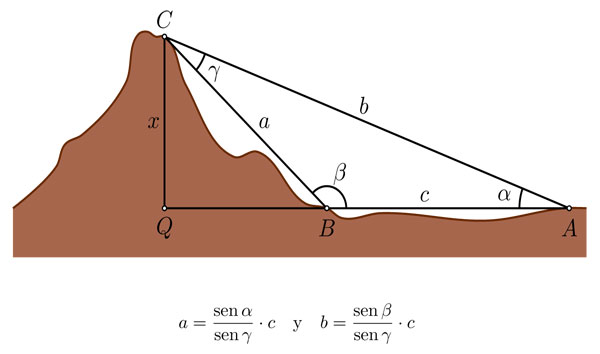
donde γ es el ángulo en C , que se obtiene a partir de α y β, pues los tres suman 180°. Conociendo b —y suponiendo que A y B están al mismo nivel—, podemos calcular la altura de C usando la definición del seno:
x = b sen α.
Con las mismas ideas que hemos considerado en esta sección, funciona el método de triangulación: primero, se mide una longitud con mucha precisión llamada "base"; después se miden los ángulos hacia un punto muy visible. Al usar la ley de los senos se pueden calcular las distancias a los extremos de la base. Como las herramientas de medición permiten medir el ángulo de elevación por separado del ángulo de giro, también es posible calcular la altura del punto visible. Después, el equipo se transporta a este punto y divisa la base y otros puntos nuevos. Así, la medición avanza por el terreno midiendo la forma de manera precisa. Gauss condujo así la medición del Hannover, y a finales del siglo XVIII, con este método, se determinó que el Popocatépetl no era la montaña más alta de México, sino el Pico de Orizaba.
