El ámbito de la producción industrial a principios del siglo xix demandaba herramientas de medición cada vez más sofisticadas. Entre los hombres que trataron de cumplir esta demanda se encontraba el matemático suizo Jakob Amsler-Laffon, quien fundó su propia fábrica de instrumentos de medición. Uno de sus más apreciados inventos fue el "integrador": un arreglo de varas, ruedas y puntas que medía cualquier área como, por ejemplo, la sección transversal de un riel de hierro mostrada en la figura 2.28. Para medir el área se tenía que colocar el integrador sobre la hoja de dibujo y, luego, pasar una punta por el borde de la figura. Una rueda integrada al aparato registraba continuamente el área, que podía leerse al final sin problemas.
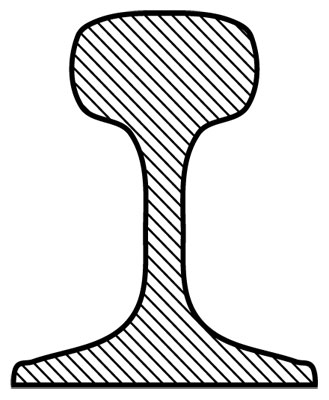
Antes de esta invención era sumamente difícil obtener una buena aproximación para el área de una figura así de compleja. Los instrumentos de Amsler se basaban de manera crucial en desarrollos matemáticos, entre ellos, el cálculo diferencial e integral. La importancia de estas herramientas no debe subestimarse: fueron fundamentales para la industria, en particular, la del acero —una buena aproximación del área de la sección transversal del riel proporciona una estimación certera del costo del material, según su peso por metro.
Es interesante ver que fue, justamente, la insistencia para calcular áreas y volúmenes de figuras —como la circunferencia— o cuerpos —como la esfera o la pirámide— lo que permitió desarrollar, poco a poco, una teoría más general que finalmente aportó herramientas matemáticas aplicables a situaciones de la vida cotidiana, como el cálculo del área de un riel que ya hemos revisado. En esta sección y en las tres subsecuentes, se exponen varios de estos cálculos con todo detalle pues, así, se logra comprender mejor las bases del cálculo integral.
Tratar de calcular el área de figuras y el volumen de cuerpos ha llamado la atención a muchas personas desde la Antigüedad. El ejemplo más famoso es, sin duda, el del área y la circunferencia de un círculo. Después de revisarlo en esta sección, sabremos cómo se puede calcular el volumen y la superficie de otros cuerpos geométricos y llegaremos a ver los fundamentos del cálculo integral en la sección 2.12.
En particular, en esta sección se verán diferentes fórmulas que expresan los volúmenes de cuerpos como prismas y pirámides. Estos cuerpos geométricos sencillos están delimitados por polígonos o figuras planas que, a la vez, están delimitados por segmentos rectos. Después, se usará esta información para determinar el volumen de una pirámide truncada —a la cual se le cortó un pedazo de la punta—. Además, se pondrá un énfasis particular en la lectura de tales fórmulas para explicar cómo las propiedades de éstas se reflejan en propiedades geométricas.
Todos sabemos calcular el volumen de una caja con lados a , b y c : V = abc, es decir, el producto de los tres lados que terminan en el vértice de la caja.
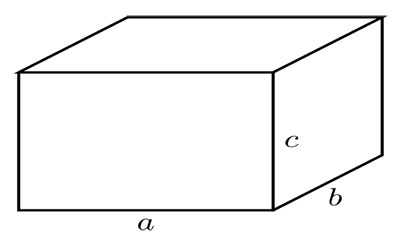
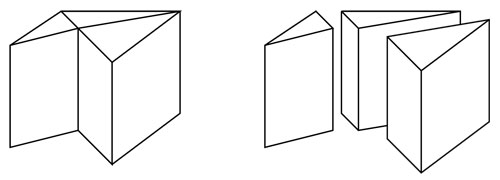
La caja tiene un nombre matemático horrible, se llama paralelepípedo rectangular y es un caso particular de un prisma. Los prismas se obtienen al trasladar un polígono en una dirección, como se muestra en el siguiente dibujo.
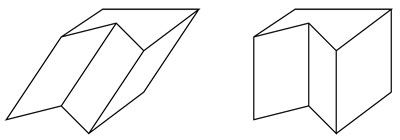
Del lado derecho vemos un prisma vertical. La fórmula del volumen de un prisma es sencilla y se parece mucho a la del rectángulo:
volumen de prisma = base × altura
sólo que aquí, "base" significa el área que se traslada y la "altura" es la distancia entre la tapa superior y la inferior. Cuidado: si al generar el prisma la base no se trasladó en dirección vertical, la altura no será la longitud de lo que se trasladó, sino menos.
Se debe observar que la dirección del traslado no importa; siempre y cuando se tenga la misma altura, se tendrán los mismos volúmenes. Esto se debe al principio de Cavalieri: dos cuerpos que tienen cortes de áreas iguales con cada plano paralelo a la superficie sobre las que están puestos, poseen volúmenes iguales.
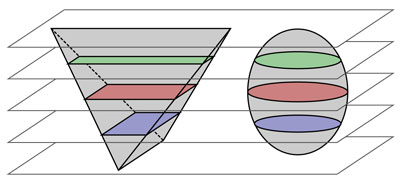
¿Cuál será entonces el volumen de una pirámide? El cuerpo se construye uniendo cada punto de la base con un punto, que es la punta de la pirámide.
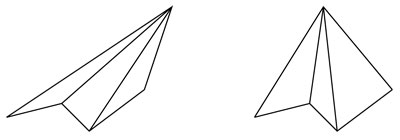
La pirámide se relaciona con el prisma como lo hace el triángulo con el paralelogramo. Se habla de una analogía, es decir, una similitud entre dos relaciones en diferentes ámbitos. Las analogías son un fuerte motor de ideas, no sólo en matemáticas, sino también en el lenguaje, por ejemplo, donde se usan para aclarar una cierta relación.
Por esta analogía, podríamos pensar que el volumen de una pirámide se calcula de manera parecida a como se obtiene el área de un triángulo: base por altura entre dos. Sin embargo, con las analogías hay que tener cuidado pues no siempre todo se traduce uno a uno de un lado al otro, la relación es usualmente más complicada.
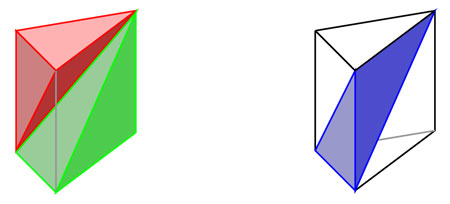
Cada prisma —o pirámide— se puede dividir en prismas —o pirámides, respectivamente— con bases triangulares y la misma altura, como se observa en la figura 2.33.
Por lo anterior, basta entender cómo se calcula el volumen de una pirámide con base triangular. Es fácil colocar dos pirámides con la misma base y altura en un prisma que también tiene la misma base y altura, como lo muestra la siguiente figura.
Como se observa, dos pirámides no son suficientes para llenar un prisma, así que la primera idea crecida sobre la tierra de la analogía no puede ser correcta. No obstante, el espacio sobrante es, a la vez, una pirámide —la base puede ser, por ejemplo, el costado vertical derecho y la altura la vemos entonces acostada en dirección horizontal.
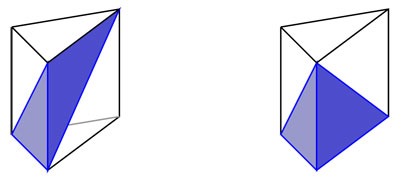
Por el mismo principio de Cavalieri, podemos mover hacia abajo la punta, que se encuentra arriba en la tapa, ya que no modificamos ni la base ni la altura. Aquí con "la base de la pirámide" nos referimos a la cara azul claro de la figura 2.35 y con "la altura" a la perpendicular —recordemos que ninguna de estas medidas depende de la dirección—. Obtenemos, entonces, que el resto también tiene el mismo volumen que buscamos. En resumen: dentro del prisma caben tres pirámides y cada una tiene el volumen de una pirámide con la misma altura y base que el prisma. Concluimos entonces que:
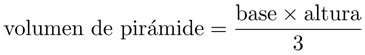
Ahora, podemos revisar la analogía de nuevo y descubrimos que sí hay una relación muy asombrosa: el 2 en el denominador se cambió a un 3 al pasar del triángulo a la pirámide. Estos números se explican en términos de la dimensión de las figuras: el triángulo es plano y tiene dimensión dos, mientras que la pirámide tiene volumen y, por ello, dimensión tres.
Recordemos que se dividió la base de cualquier pirámide en triángulos. Ahora queremos ver si podemos deducir la fórmula del volumen de cualquier pirámide. En efecto, si la base original B se dividió en t partes triangulares —B1, B2, . . . , Bt— entonces se tiene que:
B = B1 + B2 + . . . + Bt,,
lo que expresa que el área total de la base se obtiene al sumar las áreas de cada uno de los t triángulos. En forma similar:
V = V1 + V2 + . . . + Vt.
Ahora podemos sustituir cada uno de los volúmenes V1, V2, . . . , Vt por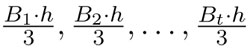 
. Así, se obtiene que:
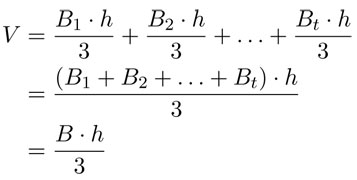
al usar la factorización en la segunda ecuación. En resumen, la fórmula que obtuvimos para pirámides con base triangular vale, en general, para cualquier pirámide.
Ahora se tienen ya conocimientos suficientes para atacar la fórmula del volumen de una pirámide truncada. Antes de entrar en cálculos y argumentaciones involucradas, observemos que la fórmula que buscamos debe "contener" la del prisma y la pirámide, como "casos particulares".
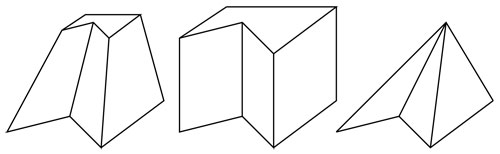
Si la base y la tapa son iguales, se trata de un prisma mientras que, si la tapa se contrae hacia un punto, resulta una pirámide. La fórmula que buscamos debe entonces "generalizar" las dos fórmulas anteriores y unirlas en una sola. Además, debe ser simétrica en la base y la tapa, es decir, si volteamos la pirámide cortada se intercambian la base y la tapa, pero el volumen no cambia; por ello, dicho intercambio no debe alterar la fórmula.
Para simplificar los cálculos que haremos a continuación, supondremos ahora que la pirámide truncada tiene como base un cuadrado de lado a , como tapa un cuadrado de lado b y la altura será denotada siempre por h .
Si la pirámide trunca se completa, obtenemos una altura H. El volumen es de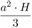 
, dado que la base tiene área a2 . Lo que se cortó al truncar es, también, una pirámide con base de área b2 y altura H − h. De esta manera, la primera fórmula sería:
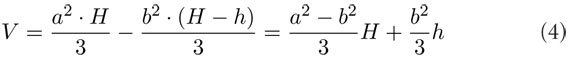
La altura H se obtiene por semejanza con:
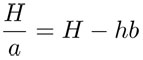
de donde, al despejar tenemos que:
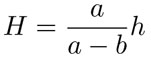
Si sustituimos H por la expresión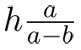 
en la fórmula (4):
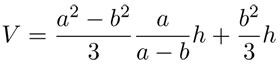
lo cual puede simplificarse en:
Ahora, si a = b resulta que a2 + ab + b2 = 3a3 y entonces, V = a2· h como lo esperábamos. Si, en cambio b = 0, entonces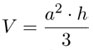 
, que también es lo que esperábamos. Se puede observar la simetría entre a y b: si intercambiamos estas dos variables obtenemos 
, lo mismo que se obtuvo en (5).
Si bien trabajamos con cuadrados para la base y la tapa, ¿cómo habría que generalizar esta última fórmula a una pirámide truncada general? Primero, observemos que a2 = B es el área de la base y b2 = T es el área de la tapa. Pero, ¿cómo habría que interpretar el término ab? Como a = √B y b = √T , entonces ab = √BT y, a partir de ahí, encontramos que:
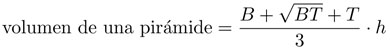
aun cuando la base y la tapa tengan una forma distinta. Todo este razonamiento se hizo a partir del principio de Cavalieri que se analizará en la sección 2.11, con mayor detalle.
