La simetría es una noción fundamental en el arte. Interviene en nuestra idea subjetiva de algo bello, pues surge de la relación que guardan las partes entre ellas y con el todo. Además, en la naturaleza hay una multitud de ejemplos donde aparece la simetría, no por consideraciones estéticas, sino por eficiencia o economía en el diseño. Más aún, ha resultado ser un elemento indispensable al considerar los modelos más avanzados de la realidad física; es una especie de principio básico en la naturaleza cuya expresión formal es, ineludiblemente, matemática.
La inmensa mayoría de los animales vertebrados tiene simetría bilateral o de espejo. Esto quiere decir que, al partirlos por un plano imaginario, las dos mitades —izquierda y derecha— se corresponden como si estuvieran reflejadas en un espejo, no de manera estricta, sino en el diseño básico o ideal de la estructura ósea y muscular. Y esto es así pues presenta enormes ventajas evolutivas en el desplazamiento, el equilibrio, el control y el desarrollo —con la mitad de los datos y una instrucción "repítase en espejo", se obtiene el todo.
También abundantes en los seres vivos, aunque más escasas, existen simetrías con mayor complejidad. Por ejemplo, en muchas flores no sólo hay un espejo de simetría, sino varios.

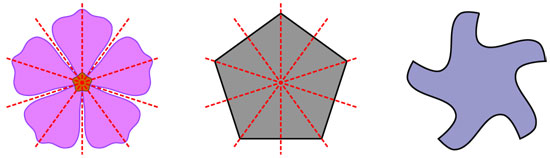
En el esquema simple de una flor de la figura 3.5, aparecen cinco posibles espejos. La simetría de su diseño es la de un pentágono regular: al reflejarlo en cualquiera de esas cinco líneas, regresa a su lugar.
Cabe aclarar que reflejar, en el sentido matemático, es la transformación del plano o del espacio en sí mismo que intercambia los dos lados de una recta o un plano, llamado espejo, y mantiene las distancias con respecto a él. En el mundo real, un espejo actúa sobre una mitad del espacio y lo hace aparecer —como visto a través de una ventana— reflejado. Pero una reflexión matemática actúa sobre ambos lados, intercambiándolos.