Además de las cinco reflexiones, en la simetría pentagonal aparecen cinco rotaciones por ángulos múltiplos de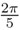 
o 72°. Hay figuras planas que sólo tienen estas rotaciones como simetrías, como se muestra a la derecha de la figura 3.4. En la figura 3.6 se observa cómo podemos distinguir estas rotaciones; para ello, se rotularon las esquinas con números, por lo que ahora es posible ver cómo se mueve la esquina número 1 bajo estas rotaciones.
A la izquierda se muestra la posición inicial, en el centro está la posición después de rotar 72° y, a la derecha, después de moverse dos veces según dicho ángulo. Hay algo importante que debe observarse aquí —aunque parezca muy simple— y que es absolutamente crucial: la rotación de la estrella ninja a la derecha en la figura 3.6 puede obtenerse como una rotación de 144° o por dos rotaciones consecutivas de 72°. Esto se puede reformular de una manera más general: dos simetrías, es decir, dos movimientos que dejan invariante a una figura pueden efectuarse uno tras otro para obtener, de nuevo, una simetría.
La figura 3.7 muestra la importancia del orden en que se efectúan dos simetrías. A la izquierda se numeran los pétalos y se muestra una rotación ρ y una reflexión σ—estas letras se leen "rho" y "sigma", respectivamente—. La flor del centro muestra el efecto de primero reflejar (σ) y después rotar (ρ) —esto se expresa en notación de funciones como ρ o σ; y se lee "rho después de sigma"— y en la tercera imagen se muestra el efecto de primero rotar y después reflejar (σ o ρ). Por ejemplo, si rotamos con ρ, el pétalo 1 queda en el lugar del 2 —podríamos escribir ρ(1) = 2, que se lee "rho de 1, o aplicado a 1, es igual a 2"—, y si después reflejamos con σ el pétalo 1 queda finalmente en el lugar donde antes estaba el pétalo 5—pues σ (2) = 5 y le da sentido a la notación (σ o ρ) (1) = σ (ρ (1)) = σ (2) = 5.
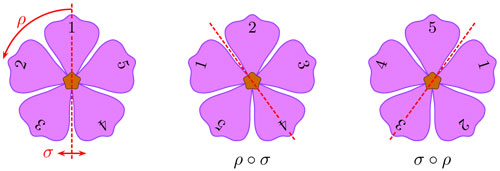
Se observa en la figura 3.7 —viendo el efecto en los pétalos numerados— que ρ o σ es lo mismo que reflejar en el eje que pasa por el pétalo marcado con el número 4, mientras σ o ρ equivale a reflejar en el eje que pasa por el pétalo 3. El proceso de efectuar primero una simetría y luego otra se llama composición. Y ahora sucede algo raro, si componemos la reflexión σ —de la figura 3.7— consigo misma, obtenemos un movimiento que no hace nada: cada pétalo regresa a su lugar. Al principio cuesta trabajo considerar al "no hacer nada" como un movimiento, pero es claramente un movimiento del plano que no altera las distancias. A este movimiento se le llama identidad, dado que funciona como el número 1 al multiplicar: deja todo como estaba.
También, cada simetría tiene su inversa: un movimiento como una reflexión o una rotación siempre tiene una reflexión —o rotación— correspondiente, que deshace el efecto del movimiento original; para las reflexiones son ellas mismas. En general, dada una simetría, la que deshace su efecto se conoce como su inversa, muy similar al hecho de que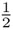 
es el inverso de 2, pues al multiplicar por 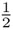se deshace el efecto de multiplicar por 2.
Por estas razones vemos que la identidad es una simetría importante y, sin ella, no podríamos componer dos simetrías cualesquiera ni podríamos considerar la formación de inversos. Las simetrías de una figura forman una estructura que se llama grupo. Los grupos tienen un elemento distinguido que es la identidad; además, sus elementos se pueden componer y se permite formar inversos.
