El Nautilus, cuya imagen inició esta sección, no tiene simetrías en el sentido de que no hay movimientos del plano como reflexiones o rotaciones que lo dejen invariante, excepto —claro está— la identidad. Sin embargo, el Nautilus tiene una forma bella y, usualmente, nuestros ojos no mienten: donde hay belleza, hay cierta simetría. En efecto, así es: el Nautilus tiene muchas simetrías, pero para verlas hay que relajar la noción de "transformación que deja invariante a la figura", a que signifique no sólo movimientos rígidos, es decir, transformaciones del plano que no alteran las distancias.
En el Nautilus necesitamos también dilataciones, es decir, transformaciones que agrandan o achican. Para tener una transformación bien definida se requiere establecer el centro de la dilatación y el factor. En la figura 3.9 vemos el ejemplo de una dilatación o, como también se les dice, homotecia.
La espiral del Nautilus tiene la propiedad de que es invariante bajo ciertas dilataciones. En la figura 3.10 se muestra una espiral particular: sobre un rayo que sale del centro —marcado con rojo— se numeraron los puntos de la espiral con …, C-1, C0, C1,…, por lo tanto, es una sucesión cuyo índice son los enteros. En esta espiral cada punto Cn está al doble de distancia al centro que el punto anterior Cn-1. Esto no depende de la dirección del rayo rojo y es igualmente cierto para otro rayo como, por ejemplo, el azul marcado en la misma figura. Por ello, una dilatación con factor 2 deja a la espiral invariante. El grupo que se forma con estas dilataciones es isomorfo al grupo de los enteros bajo la adición: al número entero n le hacemos corresponder aquella dilatación que envía el punto C0 al punto Cn.
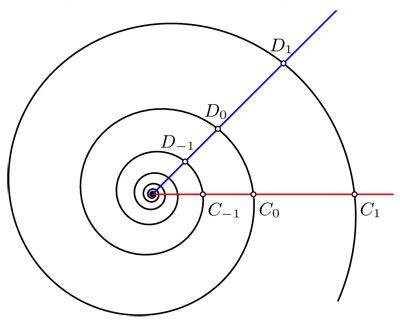
Pero éstas no son todas las simetrías de la espiral porque podemos combinar dilataciones con rotaciones. Si primero giramos de manera tal que el rayo rojo coincida con el azul y luego dilatamos por un factor apropiado, obtenemos otra simetría que manda C0 a D0. El grupo de simetría de la espiral es isomorfo al grupo de los números reales positivos bajo la multiplicación: a cada número real positivo corresponde una simetría que está compuesta por una dilatación con este factor y una rotación apropiada. Para referencia posterior, usaremos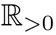 
para denotar a este grupo.
Si observamos de nuevo la imagen del Nautilus, destacan las paredes divisorias entre las cámaras internas. Si buscamos simetrías de la espiral que "respeten" también las paredes, entonces solamente ciertos factores de dilatación serían permitidos. Estos factores son de la forma ρi, es decir, son múltiplos enteros —con exponentes positivos o negativos— de un solo factor ρ. Este grupo de simetría es como el grupo de los enteros bajo la suma.
