A primera vista, la simetría es un concepto que aparece meramente de la geometría. Veremos ahora que lo anterior no es sino un punto de vista demasiado limitado. Para ello, consideramos la ecuación:
xy – 1 = 0 (1)
Esta ecuación es invariante bajo el intercambio de las dos variables x, y, dado que yx = xy. En consecuencia, si el par de números (x, y) satisface la ecuación (1), entonces también lo hace el par (y, x). Esta transformación corresponde geométricamente a una reflexión del plano en la diagonal x = y, así que esperamos que el conjunto de soluciones sea simétrico respecto a dicha reflexión. Denotemos a este intercambio como σ:
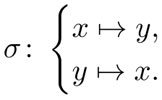
El conjunto de soluciones (x, y) describe una hipérbola con los ejes de coordenadas como asíntotas, según se muestra en la figura 3.11. En la misma figura se indica la recta x = y con color rojo. Es —como esperábamos— un eje de simetría de la hipérbola azul. También se dibujó el otro eje de simetría y = -x.
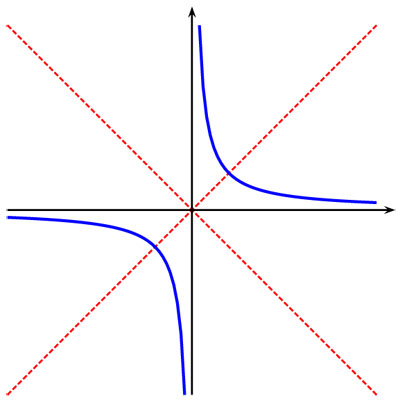
Reflejar en la recta y = -x tiene el efecto de hacer que un punto con coordenadas (x, y) sea enviado al punto (-y, -x), pues intercambia los ejes y les cambia orientación.
En otras palabras, la reflexión geométrica corresponde al intercambio de variables con cambio de signo:
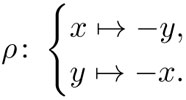
Dado que las simetrías forman un grupo, podemos componer las dos reflexiones y obtenemos una rotación de 180° con centro en el origen del sistema de coordenadas. Esta operación corresponde al cambio de signo Ƭ:
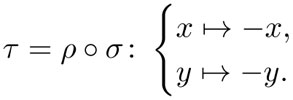
Junto con la identidad, hemos encontrado cuatro simetrías: σ, ρ, Ƭ; la siguiente tabla muestra cómo se componen estos elementos. Por ejemplo, en el segundo renglón y tercera columna —contando en lo blanco— está Ƭ, que es el resultado de componer ρ con σ —justo los encabezados amarillos correspondientes—. A esta tabla se le llama tabla de multiplicación y un grupo queda definido por ella.
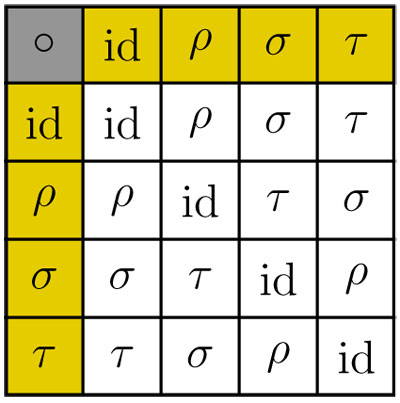
Al grupo con esta tabla de multiplicación se le conoce como el grupo de Klein. Otra realización de este grupo se obtiene al considerar entre las permutaciones de cuatro elementos 1, 2, 3, 4, sólo aquellas que permuten dos pares: por ejemplo, intercambiar 1 con 2 y al mismo tiempo 3 con 4; esta permutación se denota por (12)(34). Además de la identidad sólo hay 3 permutaciones así y éstas están determinadas por cómo se permute el número 1:
ρ = (12) (34), σ = (13) (24), Ƭ = (14)(23).
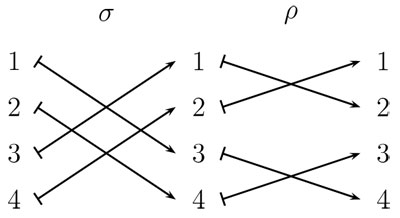
Para calcular una composición, como ρ o σ, es útil dibujar un diagrama como el que se muestra en la figura 3.12. Debe recordarse que ρ o σ denota la permutación que se obtiene al aplicar, primero σ y luego ρ, contrario a la lectura de la expresión de izquierda a derecha. Con este diagrama se verifica sin problema que ρ o σ = Ƭ y, de manera similar, se puede comprobar que las cuatro permutaciones id, ρ, σ y Ƭ, y satisfacen la misma tabla de multiplicación que las simetrías de xy = 1.
Antes de regresar a la hipérbola, vale la pena observar que el grupo de Klein también se realiza en el espacio como las simetrías rotacionales de la pelota de tenis.
En la hipérbola, y como vimos con el Nautilus, no tenemos que restringirnos a las simetrías formadas por movimientos del plano que conservan la distancia. Para cada número real positivo, la transformación:
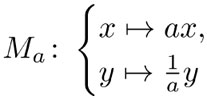
también deja invariante la ecuación de la hipérbola (1). El efecto geométrico de esta transformación es que envía un punto (x, y) al punto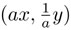 
. En particular, la recta y = x se envía a la recta 
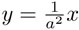. Por ejemplo, para a = 2, la transformación M2 envía la recta y = mx a la recta 
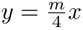, mientras que todas las hipérbolas de la forma xy = c se mantienen fijas.
El grupo formado por las transformaciones Ma es isomorfo al grupo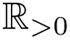 
ya que las transformaciones se componen según la siguiente ley:
Ma o Mb = Mab
Éste es el mismo grupo que el de las dilataciones del Nautilus. Si permitimos que atambién puede ser negativo, es decir, cualquier número real excepto el cero, entonces obtenemos un nuevo grupo y, si consideramos también el intercambio de x y y, obtenemos uno todavía más grande.
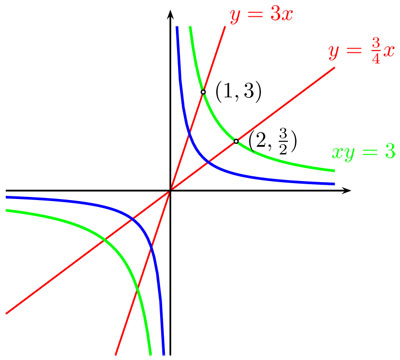
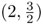. Toda la recta y = 3x es enviada a la recta 
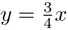, mientras la hipérbola xy = 3 permanece —como conjunto— fija.
De esta manera hemos visto que un mismo objeto puede exhibir diferentes grupos de simetría y que el mismo grupo puede aparecer en diferentes objetos.
