Existen palabras como oso, rayar o somos que pueden leerse de adelante hacia atrás o al revés y significan lo mismo. Estas palabras se llaman palíndromos. También hay frases que son palíndromos:
Anita lava la tina.
Los palíndromos tienen una simetría especial: son invariantes bajo la acción de voltearse. No se trata de una simetría geométrica, sino de cambiar de lugar letra por letra. Si aplicamos dos veces esta simetría obtenemos la identidad. El grupo es isomorfo al grupo de simetría de la galaxia y de la orquídea.
Es usual que recordemos la fórmula para calcular el área de un triángulo como "base por altura sobre dos". Pero, ¿cuál de los tres lados es la base? ¿El que está más abajo? Estrictamente, un triángulo no tiene una base, sino tres. Cualquiera de los tres lados puede fungir como base y "la altura" será, entonces, la altura correspondiente. Por ello, la fórmula mencionada anteriormente no es simétrica en las tres variables, sino que requiere una elección: hay que elegir uno de los tres lados como base.
Si tenemos un triángulo con lados de 6, 9 y 7 centímetros, no podríamos calcular con esta fórmula el área de manera directa. Por otro lado, es claro que el triángulo queda completamente definido al especificar sus tres lados y que debería ser posible calcular su área. Lo anterior se puede resolver con trigonometría, según se hizo en la sección 2.7 o con la fórmula de Herón, que dice que:
es el área del triángulo con lados , y si:
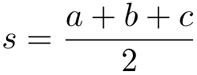
es el semiperímetro, es decir, la mitad del perímetro del triángulo. La fórmula de Herón es simétrica en los tres lados. Si permutamos los lados obtenemos una expresión que se reduce, al usar la conmutatividad de la multiplicación, a (2). Por otro lado, esta fórmula se puede evaluar simplemente: en nuestro ejemplo el semiperímetro s = 11cm es y por lo tanto:
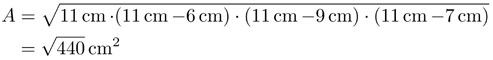
Vale la pena reflexionar sobre cuáles de las fórmulas que usualmente se aprenden en bachillerato son simétricas. Por ejemplo, el teorema de Pitágoras trata de triángulos rectángulos, cuyos lados a, b, y c no son simétricos. Uno de ellos es la hipotenusa, los otros dos son los catetos. Si c es la hipotenusa, entonces el teorema de Pitágoras afirma que:
c2 = a2 + b2,
una fórmula que "es simétrica en a y b", es decir, podemos intercambiar a y b sin alterar la fórmula. Si el triángulo no es rectángulo hay una fórmula similar que toma en cuenta el valor del ángulo opuesto al lado c, que según la convención de Euler se denota por ϒ. Esta fórmula se llama ley del coseno y dice que:
c2 = a2 + b2 – 2ab cos (ϒ)
El coseno de 90° es cero, por lo que vemos que la ley de coseno se especializa en el teorema de Pitágoras, o dicho de otra manera, la ley del coseno contiene como un caso particular al teorema de Pitágoras. Nuevamente, la ley del coseno es simétrica en a y b.
Si f y g son dos funciones, entonces la derivada de la suma o del producto es simétrica en f y g:
(f + g)' = f' + g'
(f ∙ g)' = f∙g' + f' ∙ g
donde denotamos la derivada de una función con una prima, es decir f' es la derivada de f —aquí no importa la definición precisa de derivada sino las propiedades que debe heredar de las que tienen las funciones. Esta simetría corresponde a que f + g = g + f y f ∙ g = g ∙ f, es decir, la conmutatividad de la suma y la multiplicación de funciones. Pero la derivada de la composición de funciones no es simétrica en f y g:
(g o f)' = (g' o f) ∙ f'
y ello corresponde al hecho de que la composición de funciones no es conmutativa: si f (x) = x2 y g(x) = 2x, entonces (f o g) (x) = (2x)2 mientras que (g o f) (x) = 2x2, que no es lo mismo.