En general, modelamos el mundo en que vivimos como un espacio euclidiano de tres dimensiones. Aunque la teoría de la relatividad apunta en la dirección de que el espacio físico puede no ser euclidiano —podría tener cuatro dimensiones, ser curvo y quizás hasta finito—, nuestro modelo cotidiano del espacio físico es euclidiano, de tres dimensiones e infinito. ¿Qué significa esto? Pues que la posición de cada objeto queda perfectamente especificada mediante tres números x, y, z a partir de un sistema de coordenadas que podemos fijar arbitrariamente en cualquier sitio, con cualquier orientación y con cualquier unidad de medida.
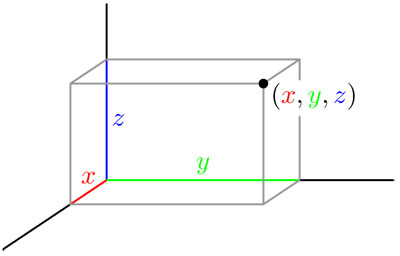
Por supuesto, los números x, y, z que dan la posición de un punto, dependen de dónde se haya colocado el origen del sistema, cómo se haya orientado y qué unidad se haya elegido. Pero una vez definidas estas variables, la posición de cada punto queda determinada de manera inequívoca mediante una terna ordenada (x, y, x) de números. Que este modelo del espacio sea "correcto" o sólo una buena aproximación a la realidad es una cuestión que corresponde resolver a la física, pero el modelo es claro y se ajusta perfectamente a la realidad cotidiana y a la mayor parte del ámbito científico. Sólo haría falta modificar este modelo utilizando el de la Teoría de la Relatividad, cuando se trata con cuestiones del espacio astronómico donde las distancias, las velocidades y las fuerzas pueden ser mucho mayores que aquellas con las que lidiamos cada día aquí en la Tierra.
La idea de los sistemas de coordenadas proviene de René Descartes, que en su libro La geometría propone este modelo para el espacio físico. Descartes no hizo más que plantear el modelo explícitamente pues éste ya existía en la mente humana y se usaba diariamente desde la Antigüedad. Para que el modelo cartesiano quede claro es necesario suponer que contamos con un sistema de numeración que permite asignar números a las coordenadas de cada punto del espacio. En particular, esto requiere que contemos con un modelo de la recta que permita asignar a cada uno de sus puntos un número.