Para modelar el continuo se utiliza el sistema numérico de los números reales que, si bien fue utilizado implícitamente por los matemáticos griegos, no se definió con precisión hasta el siglo XIX, muchos años después de que Descartes propusiera su modelo del espacio. Los hombres de ciencia y el público en general ya tenían —desde mucho tiempo atrás— una idea intuitiva del continuo, de que el espacio no puede ser modelado con algo discreto y finito, sino que hace falta considerar que entre dos puntos hay una infinidad de otros puntos y que, por lo tanto, cada punto debe tener un tamaño nulo pues, de otra manera, se podría cubrir un intervalo con un número finito de puntos. Las ideas sobre el continuo provienen de la Antigüedad y siempre causaron controversias intelectuales, como las famosas paradojas de Zenón, según las cuales sería imposible el movimiento. Por ejemplo, una de ellas dice que:
Una persona no puede recorrer una cierta distancia, porque primero debe llegar a la mitad de ésta, antes a la mitad de la mitad y, antes aun, debería recorrer la mitad de la mitad de la mitad y así indefinidamente.
De este modo, en teoría, una persona no puede recorrer una distancia, aunque la experiencia muestra que el movimiento sí es posible.
La paradoja se resuelve eliminando la hipótesis —implícita en el lenguaje— de que para realizar una infinidad de pasos es necesario un tiempo infinito. Todos los pasos pueden llevarse a cabo en un tiempo finito, porque cada uno es menor que el anterior y la suma de todos ellos es una cantidad infinita. Por ejemplo, la suma infinita de un medio de una unidad, más la mitad de un medio de la unidad, más la mitad de la mitad de un medio de la unidad, etc., es igual a una unidad. En símbolos, se representa como:
y gráficamente como:
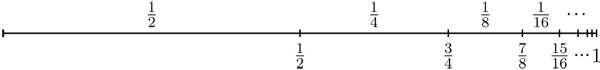
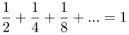
Un poco de álgebra nos permite demostrar que:
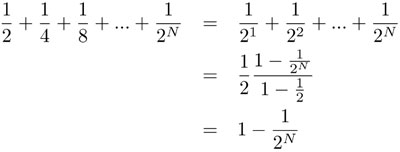
y, por lo tanto, todas las sumas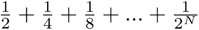 
están acotadas por 1 y tienden a 1 cuando N tiende a infinito.
Como ya se dijo en el tema 2, concebimos a la línea recta como algo continuo, sin huecos, donde en cada intervalo existe una infinidad de puntos y donde, entre cada dos puntos, existen otros. Para representar todos los puntos de una línea recta usamos los números reales. Por lo general, representamos al continuo como una recta horizontal, elegimos un punto en ella que llamamos origen e identificamos con el cero y marcamos otro punto a la derecha que identificaremos con el uno. La distancia entre el origen y este segundo punto se toma como la unidad para medir distancias.
Dada esta construcción, podemos asignar un número real a cada punto P de la recta. Para ello, contamos el número de unidades a la derecha o a la izquierda que pueden colocarse desde el origen hasta el punto y asignamos este número entero, 2 en el caso ilustrado en la figura, como primera aproximación en la representación que haremos del punto P.
A continuación, dividimos el intervalo de longitud uno en el que se encuentra el punto —en este caso, entre 2 y 3— en diez partes iguales y contamos cuántas de esas partes están a la izquierda del punto y, así, definimos el primer decimal. En este caso, obtenemos 2.4 como segunda aproximación a P. Luego dividimos el intervalo de un décimo de unidad en el que se encuentra P en diez partes iguales y contamos cuántas caben antes del punto, con lo cual definimos el segundo decimal. Continuamos este proceso indefinidamente para completar la definición del número real que representa al punto P.
La descripción contenida en el párrafo anterior es la clave del concepto de número real. Dice que el proceso continúa indefinidamente, es decir, que nunca termina. De acuerdo con nuestro lenguaje ordinario, esto parecería indicar que nunca terminaremos de definir el número. Sin embargo, con las instrucciones dadas el número ya queda perfectamente definido, pues nos permiten escribir una aproximación decimal del punto tan precisa como deseemos y eso es precisamente lo que entendemos por número real. Preocuparse porque esta definición no ofrece una expresión infinita no nos lleva a ningún lado. En general, un punto de la recta requeriría, para ser representado mediante una expresión decimal, de una cadena infinitamente larga de dígitos. Sin embargo, como por lo general esto es imposible, no tiene caso intentarlo; para considerar que el número está definido, basta describir el proceso mediante el cual se puede encontrar cada uno de sus decimales.
La representación del continuo espacial mediante números nos obliga a la creación del concepto de número real como un proceso infinito de aproximación y no como un resultado que puede exhibirse explícitamente. Se trata de algo incómodo al principio, pero perfectamente correcto desde un punto de vista lógico y, por tanto, algo a lo que la mente humana puede habituarse y manipular sin ambigüedades. La creación de los números reales permite aplicar las matemáticas no sólo a la descripción del espacio físico, sino también a la del tiempo y al estudio del movimiento de los cuerpos en el espacio, lo cual puede considerarse como el origen de la ciencia cuantitativa.
Al igual que el espacio, el tiempo también requiere del concepto del continuo y se beneficia del concepto de número real. En efecto, la observación del movimiento nos indica una continuidad en el flujo del tiempo. Cuando algo se mueve no pasa instantáneamente de una posición a otra, sino que va cambiando continuamente su posición, pasando por todos los puntos intermedios y haciéndolo en instantes intermedios entre el inicio y el final. Es perfectamente concebible un mundo en que el tiempo fuera discreto, donde todo ocurriera como en los fotogramas de una película. Sin embargo, nuestra experiencia indica que si hubiera alguna granularidad en el tiempo, ésta sería tan pequeña que no podríamos distinguirla y, dado que el espacio parece continuo y ya nos acostumbramos a esa idea, resulta natural concebir al tiempo como un continuo y representarlo con números reales.
Para medir el tiempo también se elige un origen, es decir, un evento o acontecimiento que ocurre en un instante preciso, por ejemplo, el nacimiento de Cristo o el momento en que damos el disparo de salida para una competencia deportiva. También se requiere de una unidad, que debe ser el tiempo que pasa entre dos eventos repetibles. Hay una unidad muy natural para el tiempo que casi todas las civilizaciones han tomado como unidad: el día o el lapso que tarda el Sol desde que asoma por el horizonte, hasta que vuelve a asomar por el mismo lugar al día siguiente. Las otras unidades de tiempo que se utilizan son fracciones enteras del día. La hora es la veinticuatroava parte del día, el minuto la sesentava parte de la hora, etcétera. Conviene observar que estas unidades de tiempo sólo tienen sentido en la Tierra; unos extraterrestres, si existieran, usarían con seguridad unidades diferentes para medir el tiempo y las distancias espaciales, simplemente porque no nos hemos puesto de acuerdo con ellos en una medida común. Las unidades son arbitrarias pero imprescindibles para aritmetizar el espacio y el tiempo. Las unidades de medida que puedan usar otros pueblos o civilizaciones tendrán necesariamente una equivalencia con las nuestras. Quizá algunos extraterrestres usen como unidad del tiempo una que para nosotros equivalga, por ejemplo, a 32.27 horas y quizás algún "pueblo bárbaro" se empeñe en usar una unidad de distancia que equivalga a 1 609 de nuestros metros.
