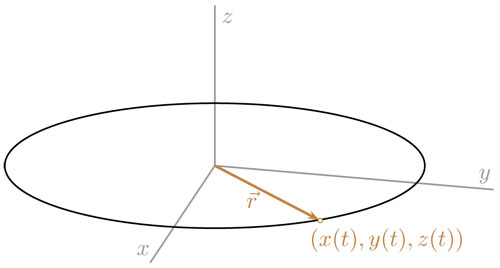
Los objetos pueden moverse, esto quiere decir que en cada momento el cuerpo puede ocupar una posición diferente. Gracias a que podemos describir la posición y el tiempo con números, también podemos describir matemáticamente el movimiento. Consideremos un cuerpo relativamente pequeño, que suele llamarse partícula, que se mueve de una posición a otra en un intervalo de tiempo. Sean t1 y t2 los instantes de tiempo al inicio y al final del movimiento, y sean (x1, y1 y z1) y (x2, y2, z2) las posiciones inicial y final de la partícula.
Esta situación puede representarse matemáticamente mediante una función del tiempo al espacio, concretamente, una función que asocia a cada instante de tiempo t una posición (x, y, z). Una función así puede representar no sólo el inicio y el final del movimiento, sino todo el recorrido. Llamemos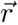 
a la función que asigna a cada instante de tiempo t del intervalo [t1, t2], la posición (x, y, z) de la partícula en ese instante. Entonces, esta función debe cumplir ciertas condiciones. En primer lugar 
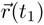debe ser (x1, y1, z1) y 
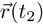debe ser (x2, y2, z2). En segundo lugar, la función 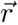debe ser continua, es decir, no debe dar saltos sino llevar el punto (x1, y1, z1) al punto (x2, y2, z2) a lo largo de una trayectoria continua, como el arco que se muestra en la figura.
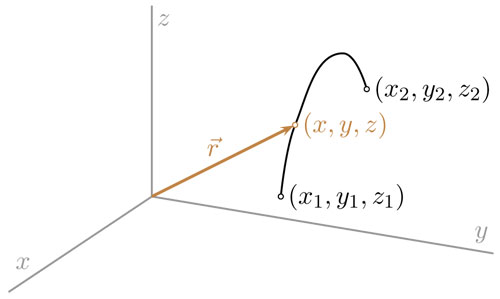
Una función así puede construirse con tres funciones continuas x(t), y(t), z(t) reales de variable real, definidas en el intervalo [t1, t2]. De esta manera es posible definir con toda precisión el movimiento de una partícula a través del espacio. La función —vectorial— 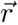, o bien las funciones escalares x(t),y(t), z(t), determinan completamente el movimiento y se llaman ecuaciones paramétricas, en las que el parámetro es el tiempo.
Por ejemplo, el movimiento de una piedra lanzada desde el origen puede representarse con las siguientes funciones:
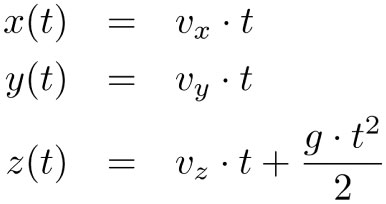
donde t representa el tiempo transcurrido desde que se lanzó la piedra y vx, vy y uz son las componentes de la velocidad inicial en las direcciones de los ejes coordenados. Otro ejemplo, serían las funciones:
que representan un movimiento circular uniforme, a lo largo de una circunferencia de radio r que yace en el plano horizontal, de una partícula que gira a razón de w radianes por unidad de tiempo.
