Si conocemos las ecuaciones paramétricas del movimiento de un cuerpo, ¿podemos determinar su velocidad en cada instante? Esta pregunta, aparentemente sencilla, dio lugar a que Isaac Newton creara el cálculo diferencial. La velocidad de un cuerpo se define como el cociente de la distancia que cubre dividido por el tiempo que tarda en recorrerla. Ésta es una definición adecuada de velocidad para un cuerpo que se mueve con velocidad constante a lo largo de una línea recta. Sin embargo, para un cuerpo que se mueve a lo largo de una curva, el concepto de velocidad es más complicado por dos razones: en primer lugar, necesitamos que la velocidad indique no sólo cuán rápido se mueve sino en qué dirección lo hace; en segundo lugar, la velocidad puede ser distinta en distintos momentos durante el movimiento, por lo tanto, hace falta definir el concepto de velocidad instantánea. El concepto de velocidad requiere de una definición precisa y rigurosa que satisfaga la noción intuitiva que tenemos de ella.
La manera en que se define la velocidad instantánea v(t)en el instante t, es con un límite, específicamente, como el límite de los cocientes del desplazamiento del cuerpo en un intervalo de tiempo [t,t + h], dividido entre el tamaño h de ese intervalo, cuando h tiende a cero. En símbolos, lo anterior se escribe así:
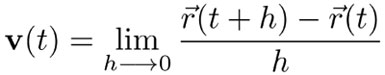
Newton llamaba a esto la fluxión de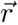 
; hoy día se le llama la derivada de 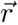con respecto a t.
Dada una función cualquiera f de una variable x, la derivada de f en el punto x se denota por f' (x) o por y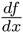 
se define como:
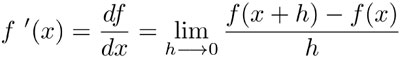
siempre y cuando este límite exista. La definición es muy general y aplica cuando los valores de f son números reales, pero también cuando son vectores en el espacio de tres dimensiones e, incluso, puede extenderse a funciones con valores en espacios mucho más generales —llamados espacios vectoriales topológicos.
El concepto de derivada de una función tiene dos aplicaciones principales, una es la que generó el propio concepto de derivada, es decir, la velocidad instantánea, y la otra es la que está relacionada con la gráfica de una función f, que tiene valores reales. La derivada de la función en un punto x viene a ser la pendiente de la recta tangente a la gráfica de la función en el punto (x, f(x)), como se indica en la figura 3.22.
Esto se debe a que los cocientes:
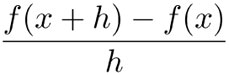
son iguales a la pendiente de la recta —llamada secante—, que pasa por los puntos (x, f (x)) y (x + h, f (x + h)).
Para obtener las derivadas de las funciones, hay que calcular los límites correspondientes. Calculemos, por ejemplo, la derivada de x3:
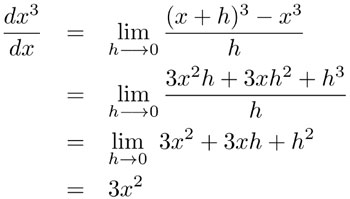
Aunque el cálculo de la derivada de una función no suele ser muy complicado si uno tiene claro el concepto de límite, es conveniente memorizar las derivadas de las funciones más frecuentes, como las que aparecen en la siguiente tabla:
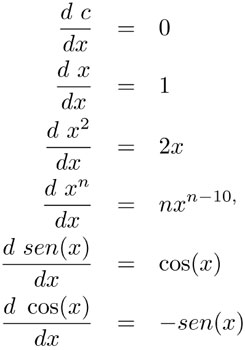
También es importante saber las reglas que se aplican al derivar sumas y productos de funciones. Sean f y g dos funciones cualesquiera, entonces:
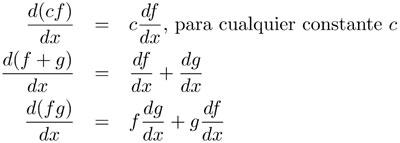
Con estas pocas fórmulas y reglas se pueden obtener las derivadas de muchas funciones. Los cursos de cálculo suelen dedicar bastante atención a que los alumnos aprendan a obtener derivadas. En ocasiones, se usan otras pocas fórmulas que aparecen en las tablas de derivación de los libros. Sabiendo derivar se pueden resolver muchos problemas como, por ejemplo, saber la velocidad instantánea de una partícula dada su ecuación de movimiento. En particular, si regresamos al ejemplo del movimiento circular uniforme descrito por las ecuaciones paramétricas:
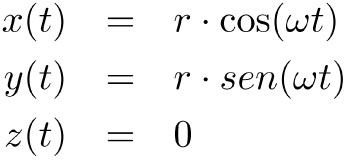
podemos obtener las tres coordenadas del vector velocidad derivando las ecuaciones con respecto a t:
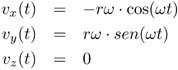
y, si volvemos a derivar con respecto a t, obtenemos las componentes de lo que se llama el vector aceleración:
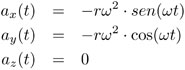
La aceleración y no la velocidad es lo que se relaciona directamente con la fuerza que se aplica a un cuerpo, esto es, el contenido de la segunda ley de Newton. Es interesante observar que el vector aceleración 
en este caso es proporcional al vector de posición 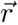, concretamente:
En otras palabras, la aceleración de un cuerpo en movimiento circular uniforme es hacia el centro de su trayectoria circular y de magnitud igual al radio multiplicado por w2, el cuadrado de la velocidad angular. Por lo tanto, si un cuerpo sigue un movimiento circular uniforme, es porque hay una fuerza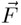 
—llamada fuerza centrípeta— que lo impulsa hacia el centro de la trayectoria:
Recordemos al lector que en el tema 1 de este libro hay una deducción de la tercera ley de Kepler basada en este resultado.
De manera similar se pueden obtener muchos resultados útiles sobre el movimiento de los cuerpos utilizando las derivadas.
