La segunda ley de Newton nos permite encontrar la trayectoria de una partícula si sabemos las fuerzas que actúan sobre ella. Sin embargo, esto no siempre resulta fácil. Poder resolver este tipo de problemas fue una de las principales motivaciones de Newton para desarrollar el cálculo integral. Si conocemos la fuerza que actúa sobre una partícula, por la segunda ley de Newton, sabemos cuáles son los valores de la aceleración, es decir, de la derivada de la velocidad con respecto al tiempo. Para obtener la velocidad de la partícula necesitamos resolver el problema inverso a la derivación, es decir, necesitamos encontrar la velocidad como una función del tiempo cuya derivada sea la aceleración que conocemos. El proceso inverso de la derivación se llama integración. Los matemáticos de la época de Newton y Leibniz, con ellos incluidos, se dieron cuenta de que la integración tenía mucho que ver con el cálculo de áreas y por ese motivo resulta conveniente comenzar el estudio de la integración con el concepto de área bajo la gráfica de una función, que se denomina integral definida.
La integral definida de una función entre dos puntos de la recta real a y b se define mediante un límite:
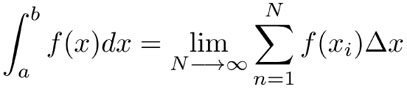(3)
donde N es un número entero positivo,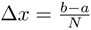 
y los valores xi son, por ejemplo, los puntos 
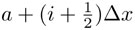que están en medio de los intervalos de ancho Δx y donde también se ha usado el símbolo ∫ llamado integral. La expresión 
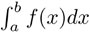se lee "la integral entre a y be de efe de equis, de equis". Obsérvese que cuando N tiende a infinito, Δx tiende a cero y viceversa; en símbolos, 
si y sólo si 
.
El límite de (3) mide el área bajo la gráfica de f (x) entre los puntos a y b, como se ilustra en la figura 3.23.
De la misma manera que el concepto de la derivada está íntimamente relacionado con su significado geométrico de ser la pendiente de la recta tangente a la gráfica de la función, la integral definida entre dos puntos a y b está íntimamente relacionada con el área delimitada por la gráfica, el eje x y los puntos a y b. De hecho, el área bajo la curva se define mediante la integral definida. Ambos conceptos, el de tangente a una curva y el de área bajo la curva, sólo pueden definirse de manera rigurosa recurriendo a los conceptos de derivada e integral definida, respectivamente.
Dada una función f(x) puede definirse otra con el área bajo la gráfica de la función entre un punto fijo a y uno variable x. En símbolos, esta función de F(x) se escribe así:
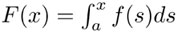
Las funciones definidas de esa manera tienen mucha importancia en las matemáticas. Por ejemplo, en la teoría de la probabilidad, si f(x) representa la densidad de probabilidad de una variable aleatoria, entonces F(x) es la probabilidad de que la variable tome valores en el intervalo [a, x]. En forma geométrica, la función F(x) definida así representa el área bajo la gráfica de f desde a hasta x y, si se concibe como una función del extremo superior de integración x, puede derivarse al igual que cualquier otra función de x, sólo que en este caso el resultado es muy interesante:
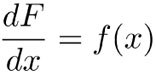
es decir, la derivación y la integración son procesos inversos uno del otro. Éste es uno de los resultados más importantes de la historia de las matemáticas pues ha permitido hacer cálculos exactos de muchos procesos límite que, de otra manera, sólo hubieran podido obtenerse en forma aproximada. El nombre de cálculo que se da al estudio de las derivadas, las integrales y su íntima relación, se debe precisamente a que dicho estudio ofrece una metodología muy poderosa para realizar cálculos en campos muy diversos como la física, la geometría y la probabilidad.
El teorema fundamental del cálculo exhibe la relación íntima que hay entre las integrales y las derivadas. Muestra que los procesos de integración y derivación son cada uno el inverso del otro. El teorema tiene dos versiones:
1] La derivada de la función 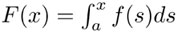es igual a f(x). Es fácil entender por qué esto es cierto si aplicamos la definición de derivada a la función F(x):
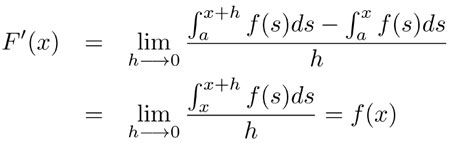
en donde hemos interpretado el primer numerador como una diferencia de áreas y lo hemos escrito como una integral definida entre x y x + h, y luego, hemos aprovechado el hecho de que cuando h es muy pequeño,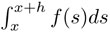 
es casi igual a f(x)h.
La segunda forma del teorema fundamental dice que:
2] Si la derivada de una función F(x) es otra función f(x), entonces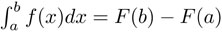 
. Para entender intuitivamente por qué ocurre esto, conviene remplazar la integral por una suma ya muy cercana a ella, digamos 
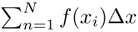, y sustituir f(xi) por el cociente:
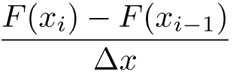
donde xi = a +iΔx. La suma puede escribirse entonces como:
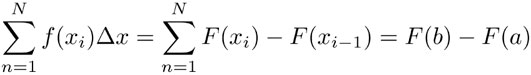
puesto que los términos F(xi) se cancelan por aparecer una vez con signo positivo y otra con signo negativo, así que sólo sobreviven los correspondientes a los extremos a y b.
Volvamos a considerar las funciones que se definen usando la integral así: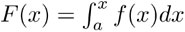 
. Diferentes puntos fijos de inicio, digamos a1 y b2, dan lugar a diferentes funciones y pero tales funciones 
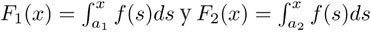y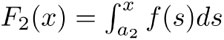 
difieren entre sí sólo por una constante, que es precisamente igual al área bajo la gráfica de la función entre los puntos a1 y a2. Las funciones cuya derivada es f(x) se llaman primitivas o antiderivadas de f. También se dice de ellas que son la integral indefinida de f, lo cual se escribe así:
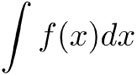
Las tablas de integrales muestran las funciones primitivas, antiderivadas o integrales indefinidas de varias funciones. La tabla siguiente es una pequeña muestra, donde c es una constante arbitraria:
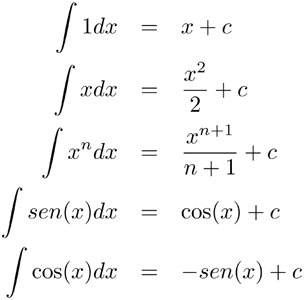
Las tablas de integrales pueden obtenerse de las tablas de derivadas. Cada fórmula de derivación nos da una de integración. Dado que es mucho más fácil calcular las derivadas que las integrales cuando partimos de las definiciones como límites, el teorema fundamental nos resuelve de manera muy general un problema. Nos permite usar las tablas de integración para realizar cálculos que de otra manera serían mucho más complicados. Ésta es la razón por la que el cálculo es una herramienta tan poderosa. Por ejemplo, si intentáramos calcular el área bajo la gráfica de f(x) = cos(x) entre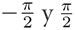 
, sin el teorema fundamental tendríamos que calcular un límite muy difícil. Pero gracias al teorema fundamental sólo necesitamos encontrar la antiderivada de f(x) = cos(x), la cual sabemos que es sen(x), y por lo tanto:
Aunque no todos los cálculos que se realizan usando la integral son tan sencillos, el teorema fundamental permite muchas veces llegar a resultados exactos que sin él serían poco menos que imposibles.
