La radiactividad es un proceso espontáneo que se presenta en la naturaleza cuando en el núcleo de un átomo ocurre un cambio. En el núcleo se encuentran partículas como los protones, con carga positiva, y los neutrones, que no tienen carga y que estabilizan a los protones. El número de protones determina las características al reaccionar con otros átomos. Es por lo anterior por lo que los átomos se clasifican en elementos como el oxígeno y el carbono que tienen, respectivamente, 8 y 6 protones. El número de neutrones puede variar. Hay átomos de carbono con 6, 7 u 8 neutrones. Esto da un total de 12, 13 y 14, respectivamente, partículas en el núcleo y, por ello, se habla de carbono 12, carbono 13 y carbono 14. Se dice que son diferentes isótopos de carbono.
El carbono 14 es radiactivo, es decir, puede decaer en cualquier momento, mientras el carbono 13 y el 12 son isótopos estables. En el carbono 14 puede suceder que uno de los neutrones se desintegre en un protón, que quede atrapado en el núcleo, y un electrón y un antineutrino que se emitan hacia el exterior del núcleo. En este cambio, el núcleo se queda con 7 protones y 7 neutrones, por lo que el átomo ahora es de nitrógeno. La cantidad de energía de las partículas que se emiten durante el decaimiento se puede medir y es lo que le dio su nombre al fenómeno: actividad en el espectro de radio, es decir, se registró la radiactividad por la radiación que emite.
Nadie puede predecir cuando un átomo de carbono 14 se desintegra pues lo hace de manera espontánea, de repente. Lo único que se puede decir es que en 5730 años hay 50% de probabilidad de que suceda y otro tanto de que no. Más sorprendente aún es que, si no decayó en estos 5730 años, tiene 5730 años para otra vuelta con una oportunidad para decaer o no del 50% - 50%. En otras palabras, los átomos de carbono 14, si no decaen, no envejecen.
Si en un momento aislamos una gran cantidad de átomos de carbono 14 y esperamos 5730 años encontraremos que más o menos la mitad de átomos ha decaído, mientras la otra mitad sigue igual. ¿Qué encontraremos otros 5730 años después? La respuesta correcta no es que ahora la otra mitad también decayó y se convirtió en nitrógeno, sino que de los átomos de carbono que sobrevivieron los primeros 5730 años, ahora la mitad también decayó. En conclusión sólo un cuarto de los átomos originales queda sin decaer y, después del tercer periodo de 5730 años, será sólo un octavo.
En nuestro ambiente hay una concentración baja de carbono 14. ¿Cómo es posible si estos isótopos decaen? ¿No tendrían que haber decaído ya todos, después de los millones de años de existencia en la Tierra? Es cierto que continuamente decaen pero, por otro lado, también se generan nuevos átomos de carbono 14 en la atmósfera alta a causa de la radiación solar. De esta manera, la concentración total se mantiene estable en nuestra atmósfera y también en los organismos pues, cada vez que respiran intercambiando gases, incorporan a su estructura estos átomos. Cuando el ser vivo muere, el intercambio cesa y los átomos de carbono 14 que quedaron integrados en su estructura hasta este momento, decaen en los milenios posteriores.
Lo anterior hace posible calcular en un resto orgánico el tiempo que transcurrió desde la muerte del organismo que lo originó al medir la concentración de carbono 14 que resta en el tejido, un método conocido como fechamiento con carbono 14. Para ver cómo funciona dicho método, veremos primero cómo depende de la concentración de carbono 14 según el tiempo —medido en años— que transcurre después de la muerte del organismo. Lo que buscamos es una función f que modele dicha concentración. De esta función sabemos que f(0) = 100% y que f(5730) = 50%. Por lo que vimos antes, tenemos que f(2∙5730) = 25%. Cada 5730 años, la concentración se divide a la mitad, así que f(3 ∙ 5 730) = 12.5%. Si escribimos los porcentajes cómo números tenemos:
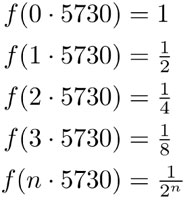
En la última línea escribimos una expresión general. Si ahora sustituimos t = n ∙5 730 y observamos que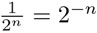 
, obtenemos la fórmula:
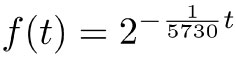
Si, por ejemplo, en un hueso se encuentra una concentración de 14.2% = 0.142, entonces debemos resolver la ecuación:
en la variable t. La figura 3.35 muestra la gráfica de esta función.
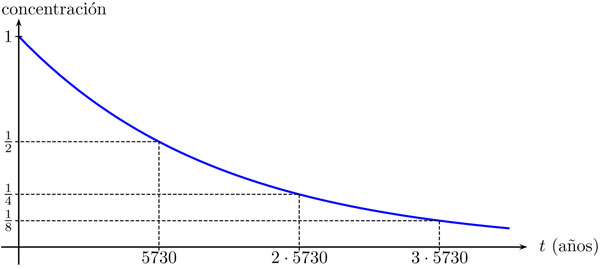
Por ello, es conveniente reescribir el lado derecho y usar la base e—el número de Euler— en vez de 2, ya que la función exp(x) = ex tiene un inverso conocido, que es el logaritmo natural In(x): si y = ex entonces x = In(y). Véase también el siguiente recuadro.
Tomamos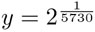 
y obtenemos un número:
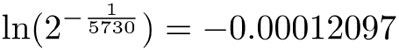
Entonces, si usamos la letra griega "lambda" para denotar a este número —es decir, λ=0.00012097—, obtenemos:
f(t) = e-λt (6)
y la ecuación que debemos resolver es:
0.142 = e-λt
o, con el logaritmo natural:
In(0.142) = -λt,
es decir:
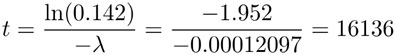
Lo cual quiere decir que el organismo del que proviene el hueso murió hace aproximadamente 16136 años.
La función (6) se llama función exponencial y se emplea con frecuencia para modelar fenómenos de la naturaleza. Lo que la función modela en este caso es el comportamiento de la concentración del carbono 14 en el tiempo; pero esta concentración no es otra cosa que la fracción de la cantidad de átomos en el tiempo entre la cantidad inicial.
En la vida real, esta función da brincos, dado que siempre hay un número entero de átomos en cada momento. Nos deberíamos preguntar si realmente es permisible usar una función continua para un fenómeno discreto; más aún, en la realidad la función depende del azar, dado que no se puede predecir cuándo los átomos decaerán. Para entender por qué la función (6) es extremadamente buena para describir el fenómeno real debe tomarse en cuenta que la cantidad de átomos que conforman la concentración es realmente enorme.
De todos los átomos de carbono en nuestro cuerpo sólo uno de un billón —un millón de millones— es un átomo de carbono 14, por lo que en un gramo de carbono hay, aproximadamente, 40 mil millones de átomos de carbono 14. Por ello, es muy improbable que no sea más o menos la mitad que decae en 5 730 años. Si sólo tuviéramos 2 átomos, la probabilidad de que la mitad decaiga es del 50%, mientras hay 25% de probabilidad de que ninguno decaiga y otros 25% de probabilidad de que ambos decaigan. Con 40 mil millones de átomos hay una probabilidad de 99.9953% de que entre 19 999 600 000 y 20 000 400 000 átomos decaigan. Por ello, la función continua aproxima muy bien el fenómeno discreto y probabilístico y el método de fechamiento con carbono 14 se puede emplear con éxito desde su desarrollo, en 1949, a partir de un equipo encabezado por el físico-químico estadunidense Willard Frank Libby.
