3.5.3 Modelos para el crecimiento poblacional

En el año 2000 había, por cada mil habitantes de la Tierra, 22 nacimientos y 9 muertos, es decir, un crecimiento de 13 personas por cada mil. ¿Cuánto tiempo transcurrirá hasta que se duplique la población si el crecimiento fuera constante a este ritmo? Es un error pensar que pasarán 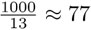años. Para entenderlo, simplificamos y digamos que pasa un cierto tiempo T hasta que la población se duplique. ¿En cuánto tiempo se habrá cuadruplicado? El tiempo necesario es sólo el doble de T ya que en cada periodo T se duplicará; por lo tanto, sólo se necesitan dos periodos. El posible error consiste en pensar que en cada año se suma la misma cantidad, cuando en realidad en cada año se multiplica por el mismo factor.

El factor de crecimiento anual λ se obtiene así: después de un año habrá por cada 1000 unas 13 personas más. Así que:

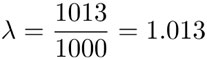
entonces, 1013 = λ ∙ 1000. Después de dos años la población habrá alcanzado λ² veces y, después de tres años, λ³ veces la población original. En la figura 3.36 se muestra cómo crece λⁿ conforme aumenta n.

Figura 3.36 Evaluación de la función 1.013ⁿ para diferentes valores de n.

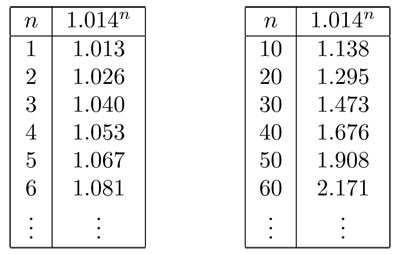
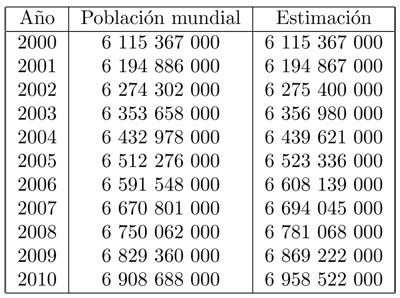
De la tabla se ve que se requieren entre 50 y 60 años para que se duplique la población mundial si sigue creciendo al mismo ritmo que lo hizo durante el año 2000. Este tipo de crecimiento se conoce como exponencial. A corto plazo, el modelo es muy exitoso, como se puede observar en la figura 3.37: la estimación no rebasa nunca el 1% de error. El modelo que se usó fue:

V(n) = V(0) ∙ λⁿ           (7)

donde λ = 1.013 y V(n) es la población en el año 2000 + n. Nuevamente, se trata de una función exponencial, pero ahora creciente.

Figura 3.37 La columna de en medio muestra los datos de las Naciones Unidas, la columna a la derecha exhibe la estimación basada en la hipótesis de que el crecimiento porcentual es constante de año en año, e igual al del año 2000. Los datos fueron redondeados a miles.

El crecimiento exponencial es ilimitado —en el modelo, la población crece y crece, rebasando cualquier límite— y, por lo tanto, inadecuado para predicciones a largo plazo: hay que tomar en cuenta que nuestros recursos son limitados, aun más, el espacio es limitado o, de manera todavía más determinante: la materia en la Tierra es infinita y hay un tiempo para el cual el modelo predice que la población rebasará aun estos límites, lo que es absurdo. Esto se conoce como la catástrofe de Malthus, llamada así por el inglés Thomas Robert Malthus, quien publicó seis ediciones de Ensayo sobre el principio de la población entre 1798 y 1826.

Por ello, en 1838, el matemático belga Pierre François Verhulst propuso un modelo que tomaba en cuenta lo limitado de los recursos y consideraba que el mundo puede sostener un máximo número de personas K—aunque este máximo sea desconocido—. Para explicar este modelo, reformulamos primero el crecimiento exponencial (7) en términos de ecuaciones diferenciales:

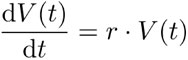         (8)

donde 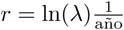; esta reformulación se justifica en el siguiente recuadro.

La modificación de (8) que propone Verhulst es introducir un término correctivo negativo :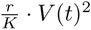

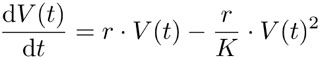         (10)

Este término de corrección depende del cuadrado de V(t) y esto tiene una buena razón: el número de encuentros en una población depende aproximadamente del cuadrado del número de integrantes, si se supone que éstos se mueven por el espacio disponible. Con los contactos, se aumenta la propagación de enfermedades, lo que disminuye la población —por ello, el término aparece con signo negativo.

Figura 3.38 El modelo de Verhulst muestra el desarrollo de la población V (t) en el tiempo de manera cualitativa, es decir, sin especificar valores concretos para y K, ya que éstos se desconocen para la población humana.

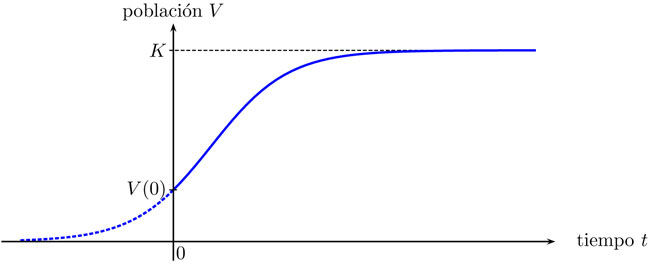
El término de corrección tiene el efecto deseado sobre el modelo: el desarrollo en el tiempo deja que V(t) se acerque a K pero sin sobrepasarlo, como se observa en la figura 3.38 y justo como se deseaba.

---