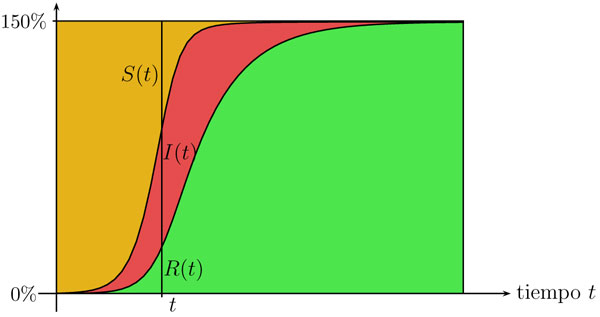
Existen muchos modelos matemáticos usados para la prevención de la salud y la estimación de cuán contagiosa es una determinada enfermedad infecciosa. Por ejemplo, se puede modelar cómo un virus —como el de la influenza— se disemina en una comunidad. En este caso se toma en cuenta que los enfermos entran en contacto con personas sanas y las contagian con el agente infeccioso. Veamos el planteamiento del modelo en forma sencilla: sea I(t) el número de personas que se han contagiado con la enfermedad como función del tiempo t y S(t) el número de personas que aún no se han enfermado. Finalmente, también habrá que considerar el número de personas R(t) que ya no se infectarán ni podrán infectar a otros: son aquellas personas que se han recuperado de la enfermedad o que han muerto a causa de ella.
Parece razonable suponer que la rapidez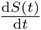 
a la que las personas sanas se enferman es proporcional al número de encuentros o interacciones entre estos dos grupos de personas. También es razonable suponer que el número de interacciones es proporcional al número de enfermos I(t)y al número de personas sanas S(t), es decir, proporcional al producto I(t) ∙ S(t), entonces:
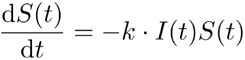(11)
donde k es la constante de proporcionalidad. El signo negativo indica que el número de personas sanas disminuye. Hay dos factores que influyen en el cambio del número de infectados: por un lado, aumenta por los nuevos infectados y, por otro, disminuye por los que se curaron o murieron. En el modelo se supone que el número de personas que deja de ser infeccioso es proporcional al número de infectados. La siguiente ecuación da cuenta de ello:
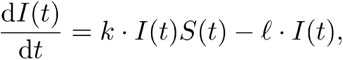(12)
Nuevamente, debe observarse los signos de los dos sumandos. Para finalizar, la tercera ecuación explicará el cambio en el número de personas que dejaron de ser infecciosas.
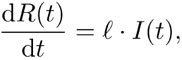(13)
Se observa que contraer la enfermedad da inmunidad a la persona, es decir, la persona ya no se puede infectar nuevamente. Las tres ecuaciones (11), (12) y (13) forman el modelo que discutimos aquí. Se trata de un modelo continuo para un fenómeno discreto: los números considerados siempre serán enteros ya que no hay fracciones de personas.
Sólo la práctica puede darnos indicaciones sobre los parámetros k y l para una población dada y un virus determinado. La correcta estimación de estos parámetros puede conducir a una predicción sobre el porcentaje de población que debe vacunarse para impedir una epidemia.
Las campañas de vacunación masiva son proyectos de la Organización Mundial de la Salud (OMS) y de muchos departamentos de salud pública. Una característica importante de las enfermedades infecciosas es la reproducción básica del factor R0, que permite estimar el número de infecciones secundarias que un individuo infectado producirá durante el tiempo en que está enfermo. Para casi cualquier enfermedad infecciosa, los modelos de ecuaciones diferenciales pueden llevar al cálculo del R0 básico al usar información específica —tal como la tasa de transmisión del patógeno, la duración del periodo infeccioso y la tasa promedio de muerte en la población—. El R0 proporciona un estimado de la situación de la infección, por ejemplo, de cómo se puede diseminar en una población sana: si el R0 es menor a uno, la enfermedad no persistirá en la población, pero si es mayor a uno, entonces la enfermedad posee el potencial para diseminarse en forma de epidemia o de volverse endémica. Un caso interesante para ejemplificar lo anterior es el de la viruela, actualmente erradicada del planeta, a pesar de que tenía un R0 de 3 a 5 y requirió vacunar alrededor del 70 u 80% de la población —el último caso de viruela se reportó en 1977—. La OMS está tratando de erradicar también la polio, que tiene un R0 de 5 a 7, lo cual significa que, aproximadamente, se requiere inmunizar entre 80 y 86% de la población mundial para lograr desaparecer la infección.
Los modelos permiten estudiar y comprender cómo es que ocurren los fenómenos que no podemos observar fácilmente o manipular directamente. Por ello, son de fundamental importancia para las ciencias. El mayor éxito entre los modelos han sido las ecuaciones diferenciales, de las cuales aquí dimos algunas muestras.
