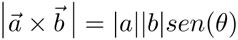Dados dos vectores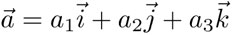 
y 
y 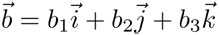un escalar —o sea, un número— C se definen cuatro operaciones algebraicas:
1] Suma de dos vectores: 
2] Multiplicación de un vector por un escalar: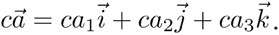 
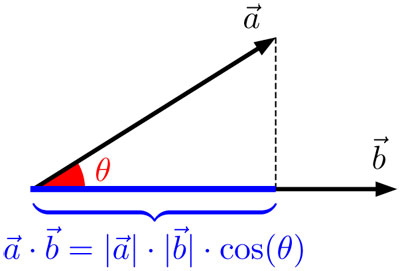
3] Producto escalar de dos vectores (también llamado producto punto):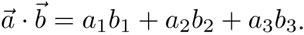 
4] Producto vectorial (o producto cruz) de dos vectores: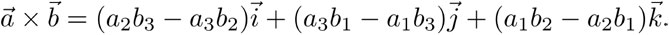 
Las primeras dos operaciones corresponden a lo que se llama álgebra lineal y las dos segundas a lo que propiamente es el álgebra vectorial. Los productos entre vectores son de gran utilidad por sus propiedades geométricas que pueden demostrarse como teoremas a partir de la definición de dichas operaciones, que describimos a continuación.
El producto escalar o producto punto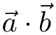 
es un número —un escalar— igual al producto de la magnitud de cualquiera de ellos por la proyección del otro sobre el primero o equivalentemente: 
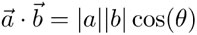, donde θ es el ángulo que forman los dos vectores.
El producto vectorial de dos vectores es un vector que apunta en la dirección perpendicular a ambos; el sentido está dado por lo que se llama la regla de la mano derecha, que dice: el producto vectorial 
apunta hacia donde lo hace el pulgar de la mano derecha cuando el dedo índice se alinea con 
y el dedo medio con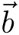 
. Finalmente, la magnitud de es igual al producto de las magnitudes de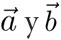 
por el seno del ángulo entre ellos:
