Los conceptos de derivada e integral que se desarrollaron para funciones de una variable, se generalizan de distintas maneras a funciones de varias variables y a campos vectoriales. Aquí nos interesan las generalizaciones de esos conceptos a funciones escalares y vectoriales de tres variables, por ser éstas de gran utilidad en el estudio de los fenómenos físicos. El teorema fundamental del cálculo tiene versiones vectoriales, muy interesantes en sí mismas y muy útiles en la física.
Estudiaremos tres conceptos que corresponden vagamente al de derivada: el gradiente, la divergencia y el rotacional. El gradiente se aplica a campos escalares, es decir, a funciones escalares f(x, y, z) definidas en alguna región del espacio de tres dimensiones. Un ejemplo de función escalar es la temperatura T(x, y, z). El concepto de gradiente corresponde al vector que apunta en la dirección y sentido del máximo crecimiento de la función y cuya magnitud es igual a la razón de cambio del valor de la función en esa dirección. Un teorema del cálculo vectorial nos dice que el gradiente grad(f), de una función f(x, y, z), que también se denota como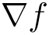 
, puede calcularse fácilmente usando las derivadas parciales de:
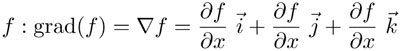
Para definir los conceptos de divergencia y rotacional es conveniente definir antes dos conceptos de integración para campos vectoriales: la integral de línea a lo largo de una curva y el flujo o integral de superficie. Definiremos estos conceptos utilizando la idea intuitiva de que la integral es una suma infinita de elementos infinitamente pequeños. Lo importante es entender qué representan los elementos que se suman y, por tanto, lo que representa cada una de esas integrales. No nos va a preocupar en este libro la formalización matemáticamente precisa de los conceptos —que por supuesto se hace usando límites—, basta decir que tal formalización puede lograrse y se puede encontrar en casi todos los libros especializados en cálculo —o análisis— vectorial.
La integral de línea del campo vectorial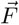 
a lo largo de una curva C se denota por:
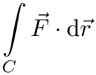
y representa la suma infinita de elementos infinitamente pequeños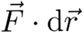 
a lo largo de la curva. Aquí, 
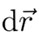representa el vector de desplazamiento infinitesimal a lo largo de la curva —en realidad, tangente a ella—. Si pensamos que 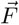es una fuerza, cada elemento 
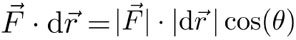representa el trabajo realizado por esa fuerza 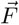a lo largo del elemento 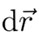de la misma —recuerda: trabajo = fuerza × distancia; la multiplicación por cos(θ) corresponde a tomar la proyección de 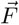a lo largo de la tangente a la curva—. Por tanto, la integral de línea puede interpretarse como el trabajo realizado por 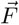sobre una partícula que se mueve a lo largo de la curva C. Cuando C es una curva cerrada, es decir, un ciclo, entonces la integral de línea se escribe así:
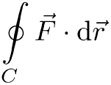
y se llama la circulación de 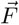a lo largo de la curva cerrada C.
El flujo de un campo vectorial 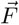a través de una superficie S se define como la integral de superficie y se denota como:
que es la suma de una infinidad de elementos infinitesimales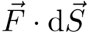 
cubriendo toda la superficie S. Los elementos 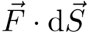son el producto escalar del vector 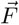por el vector 
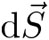que se define como perpendicular a la superficie y con magnitud igual a la del área que cubre. Las superficies se consideran orientadas y la orientación de una superficie es, precisamente, el sentido del vector perpendicular a ella. La mejor manera de interpretar el flujo de un campo vectorial a través de una superficie es pensando que el campo vectorial corresponde a la velocidad de un fluido. Entonces el flujo es la cantidad de fluido que atraviesa la superficie por unidad de tiempo.
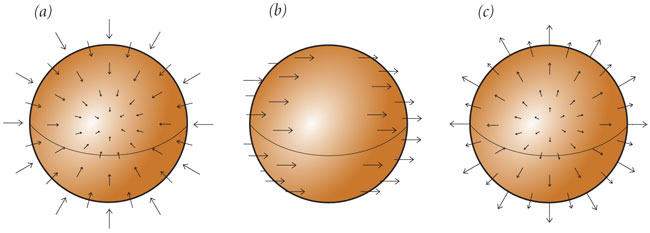
El concepto de divergencia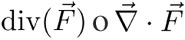 
se aplica a un campo vectorial 
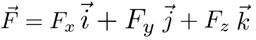. La divergencia se define como el siguiente límite, si existe:
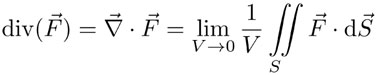
donde V representa un volumen encerrado por una superficie S. El límite se toma haciendo el volumen cada vez más pequeño, colapsándolo al punto para el que se está calculando la divergencia. Si 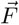representa el campo gravitatorio, resulta que la divergencia es proporcional a densidad de masa ρ:
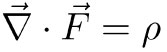
En particular, en el vacío no hay masa y, por lo tanto, la divergencia del campo gravitatorio en el vacío es cero. Algo similar ocurre para el campo eléctrico:
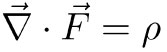
donde ρ representa en este caso la densidad de carga eléctrica. No es difícil demostrar que la divergencia de un campo vectorial puede calcularse con las derivadas parciales de sus componentes, específicamente:
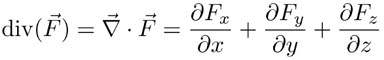
El concepto de rotacional 
también se aplica a un campo vectorial 
. Se define como otro campo vectorial que tiene la siguiente propiedad para cualquier vector unitario 
:
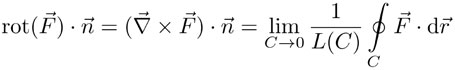
donde C es una curva cerrada sobre un plano perpendicular 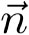a que en el límite se encoge o se colapsa a un punto. Se puede demostrar que el rotacional de un campo vectorial puede calcularse con las derivadas parciales de sus componentes, específicamente así:
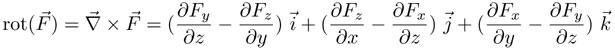
Hay tres famosos e importantes teoremas del cálculo vectorial en tres dimensiones que enunciamos a continuación.
a] Teorema de Gauss:
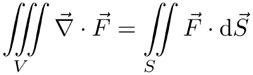
donde V es un volumen encerrado por la superficie S, lo cual se denota por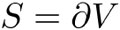 
b] Teorema de Stokes:
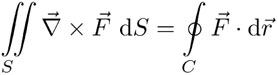
donde S es una superficie cuya frontera es la curva C, lo cual se denota por 
c] Teorema del potencial: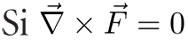 
(o equivalentemente, si 
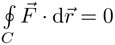para toda curva cerrada C) entonces existe un campo escalar f(x, y, z), llamado el potencial de 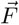, tal que:
y viceversa, si un campo vectorial es el gradiente de un potencial, entonces su rotacional es cero y las integrales de línea sobre curvas cerradas son cero.
Los dos primeros teoremas son una consecuencia más o menos directa de las definiciones de divergencia y el rotacional, respectivamente. El último es un resultado profundo que en particular nos dice que el campo gravitatorio y el campo electrostático son gradientes de un potencial. La función potencial de estos campos resulta muy útil en los cálculos. El campo magnético, en cambio, no tiene esta propiedad. El campo magnético no es el gradiente de un potencial, su rotacional no es cero y hay curvas a lo largo de las cuales la circulación del campo magnético es distinta de cero.
La siguiente sección explica las interesantes leyes del electromagnetismo, su importancia en la ciencia moderna y cómo las matemáticas jugaron un papel fundamental en el descubrimiento de las ondas electromagnéticas, que son la base de las comunicaciones modernas.
