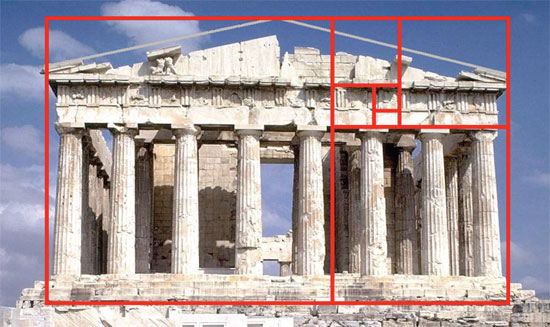
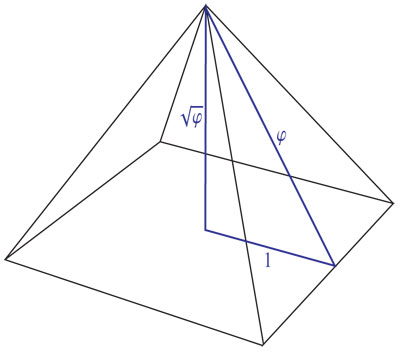
No es claro quién descubre la razón áurea y cuándo; pero es un hecho que los griegos la usaron de manera prominente en su arte y arquitectura. El nombre que seguimos usando para ella, razón o proporción "dorada", o a veces también se le llama "divina", viene desde entonces. Uno de los ejemplos emblemáticos es la fachada del Partenón en la Acrópolis, que está en Atenas, Grecia: todo el diseño arquitectónico está basado en la razón áurea, como lo demuestra la imagen de la página anterior. Pero desde mucho antes se le conocía, porque en las grandes pirámides de Egipto también se le utiliza. La gran Pirámide de Giza, muy cerca de El Cairo, tiene en su diseño central un triángulo cuya proporción de la base a la hipotenusa es áurea.
Pitágoras fue un gran estudioso de la razón áurea. Observó que las proporciones humanas tienen una estrecha relación con ella; observación que Leonardo da Vinci también documentó en el Renacimiento. Pero, ¿qué es la razón áurea?
Un rectángulo es áureo cuando al quitarle el cuadrado más grande posible (pegado a una arista corta), el rectángulo que queda tiene la misma proporción que el original.
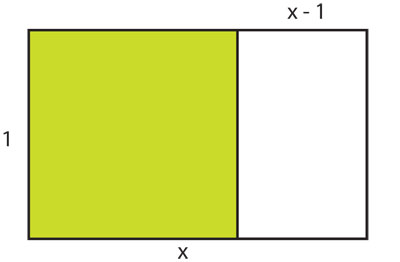
Veremos que esta propiedad da lugar a una ecuación cuadrática. Como sólo nos interesa la proporción, podemos suponer que el lado chico del rectángulo es 1. Denotemos por x (la incógnita por excelencia) al lado grande. De tal manera que el cuadrado máximo es de lado 1, y el rectángulo que sobra tiene lados x - 1(el chico) y 1 (el grande). Si éste tiene la misma proporción que el original, se cumple la ecuación:
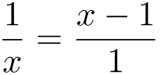
pues cada lado de la ecuación es la razón de lado chico a lado grande.
Multiplicando por x, se obtiene:
1 = x (x- 1) = x2 - x,
que equivale a la ecuación cuadrática:
x2 – x – 1 = 0. (1)
Se resuelve con la fórmula del "chicharronero" que nos da:
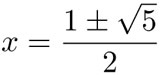
Hay dos soluciones a la ecuación (1). Cuando usamos el signo -, como 
, nos da un número negativo. Así que la solución que nos interesa es con el signo +, y podemos definir:
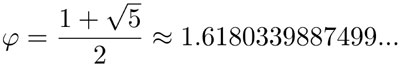(2)
donde ya estamos usando la notación común de llamar φ (es la letra griega que se lee "fi") al número áureo. Su proporción con el 1 es la razón áurea. Hemos demostrado que un rectángulo con lados a y b (con a < b) es áureo si:
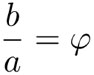
Vale la pena hacer notar que la otra solución de la ecuación (1) es – φ-1.
