Uno de los hechos que emocionaba a los griegos sobre la razón áurea, que les daba la seguridad de que su uso era trascendente y no casual, es que apareciera también en el pentágono regular: es la proporción de la diagonal al lado. Que estas dos longitudes, que surgen de un contexto tan diferente, también guarden la proporción divina, produce un estremecimiento o algo parecido al goce estético de estar ante el Partenón o ante un cuadro de Leonardo. Además, como veremos a continuación, en el razonamiento que conduce a este hecho, las piezas caen con tal precisión en el rompecabezas que es inevitable sentir "el toque mágico" de las matemáticas. No extraña, pues, que la escuela pitagórica haya adoptado al pentagrama como su símbolo, y que le hayan conferido poderes místicos.
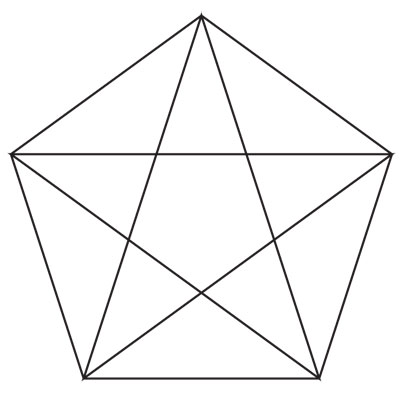
Consideremos un pentágono regular con sus cinco diagonales (figura 4.5); a veces, se le llama el pentagrama. Supongamos que sus lados miden 1 y veremos a continuación que el número áureo φ es efectivamente la longitud de las diagonales.
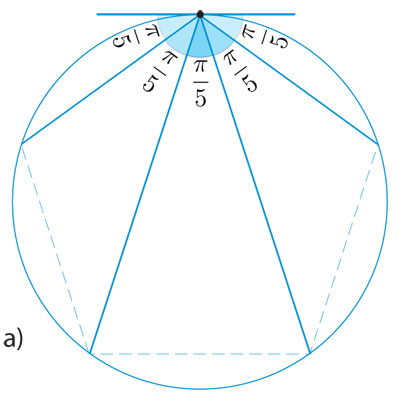
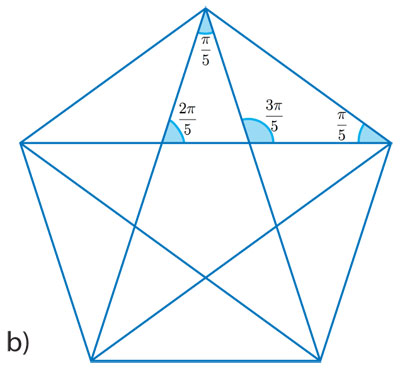
Observemos primero que todos los ángulos que aparecen en el pentagrama son múltiplos de π/5 (léase "pi-quintos") o 36 grados (aquí, es mejor medir ángulos con radianes pues los argumentos se basan en que cinco de estos ángulos dan justo media vuelta, es decir, π radianes 180 grados). Para verlo, considérense los ángulos que se forman en un vértice del pentágono, al trazar segmentos a los otros cuatro vértices y añadir su tangente al círculo que los contiene, como en la figura 4.6 a). Que los cinco ángulos que se forman son iguales, se sigue de un teorema general sobre los ángulos inscritos en un círculo, pues los cinco arcos en que se divide este último son iguales. De este hecho, y de que los ángulos de un triángulo suman π, se pueden obtener todos los ángulos que aparecen en el pentagrama en la figura 4.6 b).
Si se alargan dos lados no consecutivos del pentágono, el AC y el BD en la figura 4.7, se intersecan en un nuevo punto F.
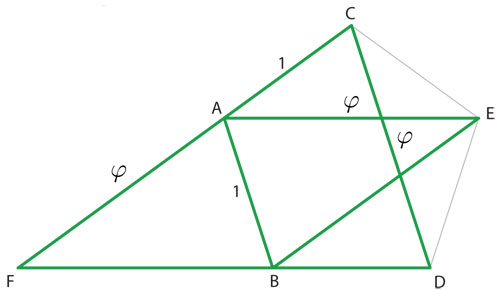
Los triángulos isósceles ABF y ABE son iguales, pues su base, que mide 1, coincide y tienen los mismos ángulos (uno de π/5 y dos de 2π/5, que se lee "dos pi-quintos"). Esto nos dice que los segmentos AF y BF miden φ (como la diagonal AE). Entonces, de la clara semejanza de los triángulos FAB y FCD, se obtiene que:
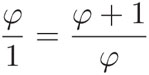
que es equivalente a la ecuación:
φ2 = φ + 1 (3)
Ésta es otra forma de escribir la ecuación (1) cuya solución positiva es el número áureo φ. Así que hemos demostrado que la diagonal de un pentágono regular está en proporción áurea con su lado.
La ecuación (3) es conocida como la ecuación áurea. Recordando que φ° = 1 y multiplicándola por φn-2 se obtiene:
φn = φn-1 + φn-2
para cualquier n positiva o negativa. En particular, se obtiene que φ = 1 + φ-1 y que 1 = φ0 = φ-1+ φ-2, de tal manera que todos los segmentos del pentagrama son potencias de φ, como se aprecia en la figura 4.8.
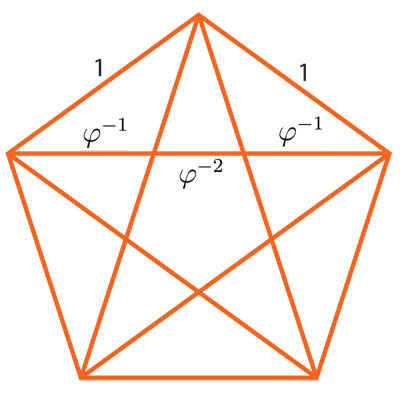
Los dos tipos de triángulos isósceles que aparecen en el pentagrama son conocidos como triángulos áureos. El alto, que usamos en la demostración, tiene dos ángulos de 2π/5 y uno de π/5; y el chaparro tiene dos ángulos de π/5 y uno de 3π/5. En el pentagrama hay cinco copias (una por arista) del triángulo áureo alto con lados 1 y φ, y diez copias del chaparro (una por vértice tanto del pentágono grande como del chiquito en el centro). Aparecen también, como sus intersecciones, copias de éstos en escalas áureas hacia abajo: diez altos y cinco chaparros con razón de semejanza φ-1 a los originales; y, por último, cinco altos en la segunda escala áurea hacia abajo, es decir, con base φ-2, que son los picos de la estrella.
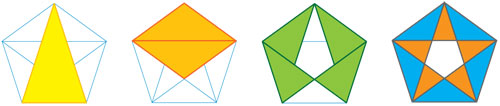
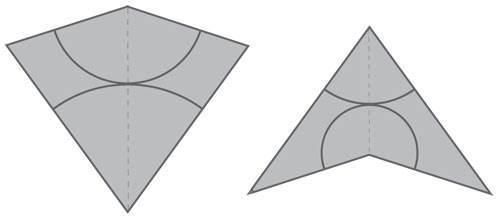
Aunque el pentagrama y los triángulos áureos han sido estudiados, apreciados y usados por milenios, siguen dando de qué hablar. Recientemente, alrededor de 1975, el físico matemático inglés Roger Penrose descubrió una familia de mosaicos íntimamente relacionados con ellos que ahora se conocen como mosaicos de Penrose. Se construyen con dos piezas: los papalotes y las dagas que, a su vez, se construyen pegando dos triángulos áureos, altos y chaparros, respectivamente. En el entendido de que cada vez que se pegan dos piezas, los extremos de las curvas de Amman coinciden (véase figura 4.10), se puede llenar to do el plano. Pero siempre da lugar a mosaicos no periódicos, es decir, que no se pueden trasladar para regresar a sí mismos. Ésta es la propiedad que ha atraído la atención de físicos y químicos en los últimos 35 años, pues están relacionados con los llamados cuasicristales. Y, por supuesto, han sido también un deleite para los matemáticos pues tienen propiedades muy interesantes; una de ellas es que la proporción de papalotes a dagas siempre es áurea.