Como sucede a menudo con conceptos fundamentales de las matemáticas, la razón áurea surge en varios contextos que, en primera instancia, parecen independientes. Uno de ellos es la famosa sucesión de Fibonacci:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, ... ,
donde cada término es la suma de los dos anteriores. Es decir, si llamamos Fn al n-ésimo (léase "enésimo") término de la sucesión, el que le sigue está definido por:
Fn+1 = Fn + Fn- 1 . (4)
En dicha ecuación (4) hay que suponer que n > 1 y declarar que los dos primeros son: F1 = F2 =1.
Fibonacci, cuyo nombre real era Leonardo de Pisa, la introduce en 1202 para estudiar la reproducción de los conejos, en un modelo muy simple que es precursor de lo que ahora se llama biología matemática o biomatemática. Aunque ahora sabemos que muchos siglos antes, los matemáticos de la India conocían esta sucesión y la usaban.
Lo que nos interesa en este momento de la sucesión de Fibonacci es que la razón entre términos consecutivos se aproxima a la razón áurea. Los primeros casos de estos cocientes son: 1/1 = 1, 2/1 = 2, 3/2 = 1.5, 5/3 = 1.666. . . , 8/5 = 1.6, 13/8 = 1.625, 21/13 = 1.6153. . . , 34/21 = 1.61904 . . . . Claramente se aproximan a φ = 1.61803 alternadamente por abajo y por arriba. Pero, al usar la notación moderna de límites, nos interesa ver que:
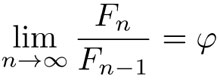(5)
Esta ecuación se lee "el límite cuando ene tiende a infinito de efe-ene sobre efe-ene-menos-1 es igual a la razón áurea"; o bien "Fn / Fn-1 tiende a φ cuando n tiende a infinito". Y quiere decir que entre más grande sea n, Fn / Fn-1 aproxima mejor a φ.
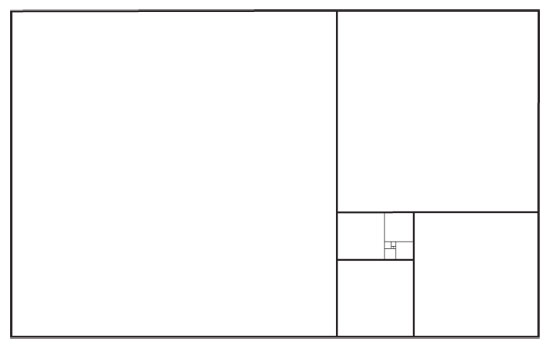
Para verlo, recordemos nuestra primera definición de razón áurea quitándole un cuadrado a un rectángulo. Podemos usarla al revés: pegándole un cuadrado a un rectángulo áureo se obtiene un rectángulo más grande pero con la misma proporción. Este proceso de pegar cuadrados se puede aplicar a cualquier rectángulo e iterarse; en esa iteración aparecerá la sucesión de Fibonacci.
Si empezamos con un cuadrado unitario, 1 x 1: al pegarle un cuadrado obtenemos un rectángulo de 1 x 2; luego le pegamos un cuadrado de 2 x 2 y obtenemos un rectángulo de 2 x 3; al pegarle un cuadrado 3 x 3, obtenemos un rectángulo de 3 x 5, y así sucesivamente (figura 4.12). Este proceso da una sucesión de rectángulos cuyos lados son términos consecutivos de la sucesión de Fibonacci.
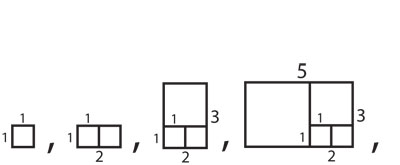
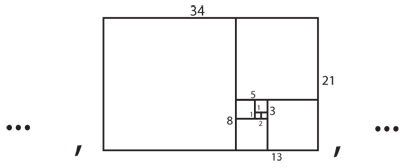
En la figura 4.12, nos saltamos tres términos y tuvimos que reducir el octavo (un rectángulo de 21 x 34) para que cupiera. Pero no importa, porque sólo nos interesan las proporciones, no los tamaños explícitos. Si de nuevo nos saltamos tres términos obtendríamos un rectángulo de 144 x 233, que al volver a reducir es casi indistinguible del áureo, pues el error, evidente en los primeros términos, se ha hecho muy pequeño. De hecho, |233/144 – φ| <0.000022.
El argumento de que el "error se hace más pequeño" conforme avanzamos en la sucesión de rectángulos, convence intuitivamente. Pero muchos matemáticos, aunque no rebatirían la veracidad de la ecuación (5), pedirían una prueba más contundente; intuirían que se puede tener más control en cómo se da la aproximación para argumentar mejor un hecho que sucede en el infinito. Puede parecer superfluo, pero esta insistencia en demostrar las cosas es lo que da solidez a las matemáticas.
Si generalizamos, al tiempo que recapacitamos en el argumento, obtendremos esa prueba. Por desgracia, puede ser que rebase el nivel de este libro pero, por las ideas que usa, puede resultar interesante y la incluimos.
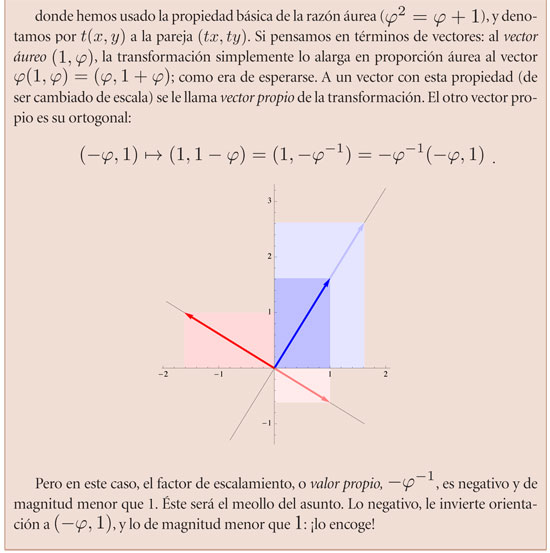Figura 4.14 Qué le hace la transformación (6) a los vectores áureos y (1, φ) y (-φ, 1).
