La ciudad de Königsberg en la antigua Prusia —que ahora se llama Kaliningrado y está en Rusia— se hizo célebre entre los matemáticos por un problema que resolvió Euler a principios del siglo XVIII. El problema era más bien un divertimento social entre los habitantes de una ciudad que se enorgullecía de sus puentes. Pero dio lugar a un desarrollo teórico que en la actualidad tiene una enorme importancia en muchas áreas de la actividad humana. El problema, juego o desafío consistía en dar un paseo por la ciudad de Königsberg de tal manera que se cruzaran sus siete puentes sin repetir ninguno. El mapa del Königsberg de aquella época está en la figura 4.17.
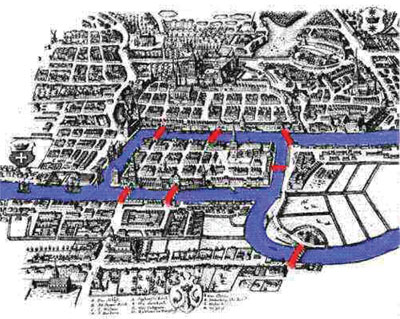
El problema se hizo famoso porque, no obstante lo sencillo de su planteamiento, nadie daba con una respuesta. La solución de Euler no es diseñar un paseo con las características que se exigen, sino demostrar y hacer evidente que es imposible hacerlo. Para entender su argumento, conviene abstraer la información esencial del problema. Son cuatro los bloques de tierra, que si representamos con pequeños círculos, que llamaremos vértices, unidos por aristas que representan a los puentes, se obtiene la gráfica de la figura 4.18.
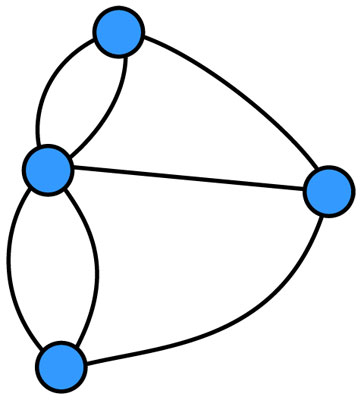
En lo que se refiere al problema, diseñar un paseo en esta gráfica, en un plano de Königsberg o echárselo a pie, en bici o en carroza por la ciudad, son equivalentes. Concentrémonos entonces en la gráfica, aunque sea válido hacer referencia a los otros dos enfoques. Un paseo consiste en una sucesión alternada de vértices y aristas que empieza y termina en vértices, en el entendido de que cada arista de la sucesión está entre los dos vértices que une —al pasear en la ciudad, cada puente comunica dos bloques de tierra—. Es decir, un paseo equivale a dibujar sobre la gráfica con un lápiz sin levantarlo nunca.
Esto remite a un problema común entre los niños de secundaria de la ciudad de México en los años cincuenta y sesenta, conocido como la firma del diablo. Consistía en dibujar un cuadrado con sus dos diagonales de un solo trazo: sin levantar el lápiz y sin dibujar sobre lo dibujado. Se insistía, para avivar la curiosidad, en que el diablo sí podía hacerlo.

Si ponemos un vértice en las cuatro esquinas y uno en el cruce del centro, el problema es equivalente al de los puentes de Königsberg; lo que ha cambiado es la gráfica en la cual se debe diseñar un paseo. Hemos generalizado el problema de los puentes de Königsberg a una familia de problemas: en cualquier gráfica se puede plantear. Y sucede muy frecuentemente que esto de generalizar ayuda a la solución.
La observación básica de Euler es que cada vez que en un paseo en una gráfica pasamos por un vértice, se usan dos de sus aristas —por la que entramos y por la que salimos—. De tal manera que si un vértice —vale la pena ponerle un nombre para referirnos a él en específico, y qué más simple que una letra—, llamémosle v—para pensar en vértice—, no es aquel donde iniciamos o concluimos un paseo que no repite aristas, entonces habremos usado un número par de las aristas que inciden en v. ¿Cuántas? Justo el doble de las veces que pasamos por v. Revisemos la gráfica de Königsberg para concluir que el paseo que se pide en el problema es imposible. En cada vértice inciden un número impar de aristas —hay un vértice con 5 aristas y tres con 3—; ninguno de ellos puede ser intermedio en un paseo que no repite aristas y las usa todas. Y el mismo argumento se aplica a la firma del diablo: hay un vértice con cuatro aristas —el del centro—, pero hay cuatro —las esquinas— con tres aristas. Faltan candidatos a ser vértices intermedios. ¡Ni el mismísimo diablo puede firmarlo!