Cuando se usa una y otra vez la misma descripción o frase, los matemáticos acostumbramos ponerle un nombre para que el discurso sea más fluido. En honor al primero que los estudió, se les llama paseos eulerianos a los paseos en una gráfica donde no se repiten aristas y además pasan por todas ellas, como los que estábamos buscando en Königsberg o en la firma del diablo. Puede haber de dos tipos: cerrado cuando el paseo empieza y acaba en el mismo vértice, o abierto cuando éstos son distintos. El otro concepto que se repite insistentemente es el del número de aristas que inciden en un vértice: llamémosle su grado. Podemos ahora limpiar y resumir el argumento de Euler.
Si una gráfica tiene un paseo euleriano cerrado, entonces todos sus vértices tienen grado par; las aristas donde se empieza y se acaba se pueden aparear para dar ahí el grado par. Pero el argumento da para más: si una gráfica tiene un paseo euleriano abierto, entonces todos sus vértices tienen grado par excepto el del principio y el del final —la arista con que empezamos y con la que acabamos no tienen con quién aparearse.
Euler, siendo un gran matemático, no se quedó satisfecho con su ingeniosa solución al problema de los puentes de Königsberg. Definió en general el concepto de gráfica como un conjunto de vértices (o nodos) junto con un conjunto de aristas, cada una de las cuales une (o incide con) dos vértices. Y se hizo la pregunta inversa: ¿será cierto que una gráfica que tiene todos los vértices de grado par admite un paseo euleriano cerrado? Y, si tiene únicamente dos vértices de grado impar, ¿tendrá un paseo euleriano abierto? Demostró que así es. Por ejemplo, si en Königsberg se construyera otro puente, cualquiera que sea, ya habría paseos eulerianos abiertos. O bien, cuando el diablo firma, pasa dos veces por una arista exterior pero lo hace con tal precisión y rapidez que no se nota el repaso.
Vale la pena reconstruir el argumento de Euler porque es indicativo del área de las matemáticas que ahora se llama combinatoria o matemática discreta.
Primero, observemos que el caso de dos vértices de grado impar se puede reducir al otro añadiendo una nueva arista entre los dos vértices especiales.
Dada una gráfica G —de nuevo será importante ponerle un nombre sencillo—, con todos sus vértices de grado par, iremos construyendo un paseo euleriano cerrado poco a poco. Pensemos que la tenemos dibujada con lápiz en un papel con circulitos de vértices y segmentos —rectos o curvos, pero simples— como aristas. Escogemos uno de sus vértices, llamémoslo v0—léase "v-cero" — y con un plumón rojo vamos recorriendo a G: armando paso a paso un paseo, con la única precaución de que no se vale pasar por una arista ya pintada de rojo (figura 4.20).
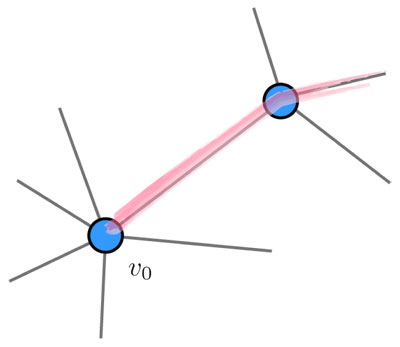
Cuando pasamos por algún vértice se marcan dos de sus aristas, así que de un vértice que no sea v0 siempre podemos salir porque su grado es par: al llegar a él hay un número impar de aristas rojas y por lo tanto queda alguna en lápiz; por ella salimos y lo volvemos a dejar con "grado rojo" —y "grado en lápiz"— par. Entonces, la única manera en que nos atoremos y no podamos seguir adelante es regresando a v0 y, además, cuando el resto de sus aristas ya son rojas (fig. 4.21).
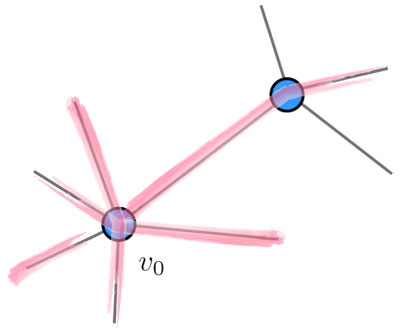
En ese punto ya no tenemos por dónde salir. Hemos construido un paseo cerrado que empieza y termina en v0 y usa todas las aristas que inciden en él. Si toda la gráfica G ya es roja, acabamos, pues estamos de suerte y, al primer intento, encontramos el paseo euleriano que buscábamos. Si no es así, quedan en G algunas aristas en lápiz y mejoraremos nuestro intento, pero usándolo como base.
Volvemos a recorrer el primer paseo —justo el mismo recorrido— hasta el momento en que lleguemos a algún vértice v1 con aristas en lápiz. Hacemos ahí una pausa. Notemos que hay un número par de aristas en lápiz en v1 —ya que hay un número par de rojas— y que en cada otro vértice también hay un número par de aristas en lápiz —que puede ser 0—. Salimos de v1 por alguna de estas aristas en lápiz y seguimos y seguimos pintando más aristas de rojo. Por la misma razón que en el caso anterior, este deambular sólo puede terminar regresando a v1 cuando todas sus aristas ya son rojas. Aquí concluye la pausa y retomamos el camino de nuestro primer paseo que termina en v0. Este nuevo paseo, basado en v0, incluye más aristas rojas que el primero.

Si no hemos pasado con el plumón rojo por todas las aristas de G, repetimos el mismo proceso pero ahora con nuestro paseo extendido como base y, así, seguimos una y otra vez. En cada vuelta ampliamos el paseo y pintamos más aristas. Y para demostrar que este proceso termina en algún momento, que el paseo se vuelve euleriano, tenemos que suponer dos cosas que no habíamos hecho explícitas. Primero, que la gráfica G —tanto vértices como aristas— es finita, lo cual sobreentendíamos al pintarla en un papel y obliga a que tiene que llegar el momento en que el paseo ya no pasa por ningún vértice con aristas en lápiz. Y segundo, que G es conexa, es decir, que no consiste en dos o más pedazos aislados, porque entonces nuestro proceso sólo pinta de rojo a la componente conexa en que vive v0 nos da un paseo euleriano en ella, pero lo demás, como no tiene manera de comunicarse con v0 a través de paseos, se queda pintada en lápiz: el plumón rojo nunca llega ahí.