Cantor descubrió que hay más que un tipo de infinitos. Demostró que los números enteros —incluyendo los negativos— tienen la misma cardinalidad que los naturales y que también los racionales tienen la misma cardinalidad. Pero los números reales, aquellos que vimos en la sección 2.3 para expresar lo continuo, tienen otra cardinalidad, una que es mayor que 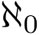 .
.
El argumento que dio Cantor se conoce hoy como el argumento diagonal y se basa en la contradicción, es decir, supone que los números reales son numerables. Si éste fuera el caso, sería posible hacer una lista completa —aunque infinita— de los números reales. A continuación, se demuestra que hay un número que no está en la lista, lo que constituye una contradicción a la suposición de que la lista era completa pues contenía todos los números reales. Como en la argumentación no hay error alguno, se concluye que la suposición fue falsa y así queda demostrado que los reales no son numerables.
Veamos ahora cómo construir el número real que no está en la lista. Para ello, se usa la misma lista que se suponía completa y se escribe cada número en su expansión decimal. Después, se construye el número en su expansión decimal al usar los dígitos que se encuentran en la diagonal de la lista. Observemos cómo podría empezar la lista —dado que los dígitos de la diagonal juegan un papel importante, se marcaron con color rojo:
 (7)
(7)
De esta manera, obtenemos una sucesión de números:
1, 3, 7, 9, 0, 1, 0, 8, 3,… (8)
Ahora bien, se construye un nuevo número x de manera que el dígito en posición n sea diferente del dígito en la misma posición de la sucesión (8). Esto se puede hacer, por ejemplo, de forma que cada dígito 1 se convierte en 0 y los otros dígitos en 1. En nuestro caso, obtendríamos:
x = 0.011110111…
Entonces, encontramos que x ≠ n1 ya que difieren en el primer dígito, que x ≠ n2 ya que difieren en el segundo y así sucesivamente. La conclusión es que x no es ningún número de la lista y la lista fue incompleta. Hemos llegado a la contradicción que buscábamos.
Cantor compara diferentes conjuntos y es capaz de mostrar que la cardinalidad de los dos conjuntos es la misma:
Los dos conjuntos describen el lado y la superficie de un cuadrado. Es decir, el conjunto de puntos de un segmento es igual que la cardinalidad de toda el área. Eso fue muy sorprendente. Con el uso de los conjuntos potencia se puede demostrar aún más: hay una infinidad de "diferentes infinitos".


Con los conjuntos potencia se muestra que hay una sucesión infinita de diferentes infinitos, cada vez más grandes.