Ya vimos que hay muchos infinitos y, con los conjuntos potencia, sabemos que podemos encontrar cardinalidades cada vez más grandes. Se escribe |X| para denotar la cardinalidad del conjunto X. En efecto, se puede mostrar que cualesquiera dos conjuntos X y Y siempre son comparables, es decir, que sólo hay tres opciones posibles: |X| < |Y| o |X| = |Y| o |X| >|Y|. En otras palabras, si las cardinalidades de X y Y no son iguales, entonces o el conjunto X tiene la misma cardinalidad que un subconjunto propio de Y o, al revés, el conjunto Y tiene la misma cardinalidad de un subconjunto propio de X. Esto no es para nada obvio y Cantor tuvo que introducir los ordinales; primero, demostró que cualesquiera dos conjuntos ordenados, siempre se pueden comparar. Como consecuencia los números cardinales, es decir, las cardinalidades siempre se pueden comparar en forma muy similar a como se comportan los números naturales o reales.
Dado que los cardinales se pueden comparar, Cantor pudo definir el cardinal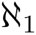 
como el primer número cardinal que es mayor que 
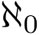. El número cardinal 
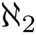es el que sigue después de 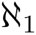, y así sucesivamente. Lo que, en cambio, no quedaba nada claro era la cardinalidad del conjunto de los números reales. Es casi seguro que Cantor pensara que los reales tienen la cardinalidad 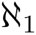, lo que hoy se conoce como la hipótesis del continuo. Pero unos 50 años después de él, se descubrió que esta pregunta es independiente del sistema de axiomas de Zermelo-Fraenkel. Como consecuencia, se puede hacer matemáticas con la hipótesis de que los reales tienen cardinalidad 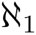o con la hipótesis de que la cardinalidad de los reales es mayor que .
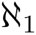Lo anterior debería ser algo inquietante pues afirma que el conjunto de los números reales no se conoce bien, ni siquiera en lo que se refiere a sus subconjuntos. No se puede determinar si hay o no un subconjunto X de números reales que tenga una cardinalidad intermedia entre los naturales y los reales o si tal subconjunto no existe.
