Galois estudia cómo ciertas permutaciones de las raíces de un polinomio, es decir, las soluciones de una ecuación algebraica, corresponden a ciertos campos intermedios —véase sección 4.9—. En lo anterior, hay dos nociones abstractas: el grupo y el campo. La formalización de estas nociones fue tardía.
Hoy se define al grupo como un conjunto G junto con una operación binaria: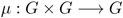 
, es decir, una función del producto cartesiano G x G al conjunto G con ciertas propiedades. El producto cartesiano G x G es, por definición, el conjunto de pares (a, b) de elementos a, b de G. En otras palabras, la función μ asigna a cada par de elementos un elemento de G.
Un ejemplo de lo anterior es la suma de números enteros que asigna a cada par de números su suma; en este caso se denota μ(a, b) = a + b.
La multiplicción y la exponencial son también otras funciones y se denotan μ(a, b) = ab y μ(a, b) = ab, respectivamente.
Para que G sea un grupo debe satisfacerse la propiedad de asociatividad, que se escribe de la siguiente manera si μ(a, b) = ab: para todo a, b, c en G se tiene (ab)c = a(bc). La segunda propiedad es en la que se pide que exista un elemento neutro e, esto es, un elemento que satisfaga ea = a = ae, para todo elemento a de G. La tercera y última propiedad que se pide es que para cada elemento a de G existe un inverso multiplicativo, es decir, un elemento b tal que ab = e = ba, donde es el elemento neutro.
Debe observarse que no se requiere que ab = ba para todo a y b de G. Si esta propiedad también se satisface, se dice que el grupo es conmutativo, o también se dice que el grupo es abeliano, en honor a Abel, quien se dio cuenta de la importancia de la conmutatividad para poder resolver una ecuación con radicales.
Algunos ejemplos de grupos conmutativos son los números enteros con la adición o los números racionales distintos de cero con la multiplicación como operación binaria. Un grupo no conmutativo es el conjunto de todas las permutaciones del conjunto I = {1, 2, 3, 4}, es decir, todas las funciones biyectivas de en I en I. La operación binaria en este caso está dada por la composición de funciones.
La segunda noción es la de campo. Un campo es —en el lenguaje moderno— un conjunto con dos operaciones que suelen denotarse como suma y multiplicación, tal que la suma es asociativa, conmutativa, admite elemento neutro 0 e inversos, mientras que la multiplicación es asociativa, conmutativa, admite elemento neutro 1 y cada elemento no cero tiene inverso multiplicativo. Ejemplos de campos así son los números racionales, los reales o los complejos, pero también campos como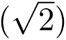 
, esto es, los números reales que tienen la forma 
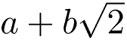con a y b racionales.
Hoy día hay teorías completas que se llaman teoría de grupos y teoría de campos, y que se dedican al estudio de cada una de estas dos nociones. Una vez que se han formulado dichas nociones es fácil obtener nuevas estructuras.
Por ejemplo, un anillo con unidad se define en forma muy similar a un campo: es un conjunto con dos operaciones binarias denotadas como suma y multiplicación, con la única diferencia de que en la multiplicación no se pide ni conmutatividad ni existencia de inversos. Ejemplos de anillos son los polinomios [x], con coeficientes racionales en la incógnita x, que se pueden sumar y multiplicar. El polinomio constante 1 es la unidad multiplicativa, pero ningún polinomio de grado positivo tiene un inverso multiplicativo.
Aunque la noción de anillo es una generalización de la de campo, la teoría de anillos es muy distinta a la teoría de campos, pues se requieren herramientas diferentes para trabajarlas. Una noción importante para la teoría de anillos es la de un ideal. Un ideal I de un anillo A es un subconjunto I ⊆ A que contiene el 0, es cerrado bajo la suma, es decir i1 + i2 es un elemento de I para cada i1 + i2 de I. Además, el inverso aditivo de cada elemento de es I, de nuevo, un elemento de I y, con respecto a la multiplicación, se tiene que para cada a de A y cada i de I, también los elementos ai, ia pertenecen a I. Para campos, el concepto de ideal no es interesante ya que siempre hay sólo dos ideales: todo el campo y {0}, el ideal cero.
Para anillos e ideales hay muchos ejemplos naturales. Por ejemplo, los polinomios de grado mayores o iguales que 3 forman un ideal de [x], o más general, para cada polinomio f de [x] los múltiplos de f, es decir, los polinomios gf—donde g es cualquier polinomio— forman un ideal que se denota por (f).
Un ideal se llama primo si satisface la siguiente propiedad: si un producto a1 a2 pertenece a I, entonces, al menos uno de los dos factores pertenece a I. Veamos esto en el ejemplo del anillo Z de los números enteros con la suma y multiplicación usual. El ideal (5) consiste en todos los múltiplos de 5 y es un ideal primo: a1 a2 si es un múltiplo de 5, entonces a1 o a2 tienen que ser múltiplos de 5. En cambio, el ideal (6) no es primo ya que el producto 2 x 3 está en (6), pero ninguno de los factores está en (6). Se ve que el ideal (f) es primo exactamente cuando el número f es primo o es cero.
La formalización de estos conceptos y la abstracción del contexto de las ecuaciones tardó más de un siglo y culminó a principios del siglo XX. En este proceso incidieron muchos matemáticos, como el inglés William Rowan Hamilton y los alemanes Ernst Eduard Kummer, Emmy Noether —una de las mujeres matemáticas más destacadas— y Emil Artin, entre muchos otros.
En 1930, el matemático Van der Waerden publicó un libro llamado Álgebra moderna, en donde, por primera vez, se definen todos estos conceptos —y muchos más— en el lenguaje que se sigue usando hasta hoy y que se basa en la teoría de conjuntos, establecida a principios del siglo XX.
